Квантовая телепортация более 100 км волоконно используя высокоэффективную сверхпроводящего нанопроволоки Детекторы однофотонные

HIROKI TAKESUE, 1, и др.

1NTT Базовая Research Laboratories, NTT корпорация,  Япония

2National институт стандартов и технологии, NIST, США

 This email address is being protected from spambots. You need JavaScript enabled to view it.

опубликовано 23 сентября 2015

Квантовая телепортация является важной квантовой операцией с помощью которой можно передать неизвестное квантовое состояние на удаленное расстояние с помощью квантовой запутанности и классическая коммуникация. С первых экспериментальных демонстраций используя фотонные кубиты и непрерывных переменных, расстояние фотонно квантовая телепортация над свободном пространстве каналов продолжает расти и достигло> 100 км. На С другой стороны, квантовая телепортация по оптическому волокну было сложной, главным образом потому,что обнаружение многократно фотон что неизбежно сопровождает квантовые эксперименты телепортации был очень неэффективным из-за относительно низкой обнаружения эффективность типичных телеком-группы однофотонной детекторы.

Здесь мы сообщаем о квантовой телепортации фотонов по оптическому волокну длиной 102 км при использовании четырех  высоко эффективных однофотонных фотодетекторов на основе сверхпроводящих нанопроволок  (SNSPDs). Эти SNSPDs позволяют выполнять высокоэффективные многократные измерения фотонов, что позволяет нам подтвердить, что квантовые состояния входных фотонов были успешно телепортированы на расстояние более 100 км  по оптическому волокну со средней достоверностью 83,7%+ 2,0%.

Квантовые коммуникации; Квантовые детекторы;  Квантовая и обработка информации.

 

В последние два десятилетия, мы видели значительный прогресс в квантовой криптографии  (QKD) и передаче излучения по оптическому волокну [1,2]. QKD более  100 км оптоволокну были достигнуты со схемами на основе ослабленного лазерного луча [3-5] и использования схем генерации  запутанных фотонов  [6]. Тем не менее, для преодоления экспоненциального падения ключевой нормы, которая вызвана  потерей в оптическом  волокне и добиться масштабируемую QKD, мы должны использовать квантовый повторитель [7,8], в котором  квантовая телепортация [9] играет решающую роль.

С первых экспериментальных демонстраций с использованием фотонных кубитов [10] и непрерывных переменных [11] на очень коротких расстояниях выполненных в  лабораторных условиях, расстояние передачи квантовой телепортации фотонов   в свободном пространстве  продолжало расти и достигло более  100 км [12,13]. С другой стороны, квантовая телепортация выполняемая по оптическому волокну являлась  сложной [14,15], в основном из-за трудности выполнения задачи многократного обнаружения фотонов, что неизбежно сопровождается в квант телепортационных экспериментах. Они были очень неэффективно из-за относительно низкой эффективности регистрации стандартных  singlephoton групп-детекторов, регистрирующих одиночные фотоны.

Поэтому было сравнительно мало работ по квантовой телепортации по оптическому волокну [14,15]. О новаторском эксперименте сообщалось в [14], там квантовые состояния по времени бин кубитов были переданы в оптическом волокне длиной 2 км. Недавний эксперимент [15], который установил рекорд расстояния для кванта телепортация по оптоволокну (длиной 25 км), реализован при использовании  квантового реле при этом конфигурация с телепортируемом фотона хранилась в квантовой памяти. Недавно, были изготовлены  фотодетекторы однофотонные (SNSPDs) на основе нанопроволок с более чем 90% -ной эффективностью обнаружения в диапазоне длин волн 1,5 мкм. Эти фотодетекторы  были сделаны с помощью сверхпроводящих нанопроволок на основе аморфного силицида вольфрама (WSI) [16]. В настоящей работе, мы использовали SNSPDs основе другого аморфного материала, силицид молибдена (MoSi), для выполнения операции фотонной квантовой телепортации по оптоволокну. Выбор MoSi вместо WSi позволил производить измерения при более высокой температуре с меньшими погрешностями (дрожаниями) [17]. Мы использовали четыре фотодетектора  с эффективностью детектирования (80% -86%) MoSi SNSPDs, что позволило нам выполнить высокоэффективную многократный совпадение измерения, полученные при успешной квантовой телепортации фотонов на расстояние более 100 км по оптическому волокну.

Здесь мы описываем экспериментальную  установку для выполнения  квантовой телепортации. В качестве квантового носителя информации мы используем фотон, которые кодируются как раз-бен кубита, который является когерентной суперпозицией два временных режимов [18]. Фотонного времени бин кубит больше подходит для передачи по оптическому волокну, чем поляризационный кубит, потому что трудно сохранить состояние поляризации в протяженном  волокне длиной 100км.

 

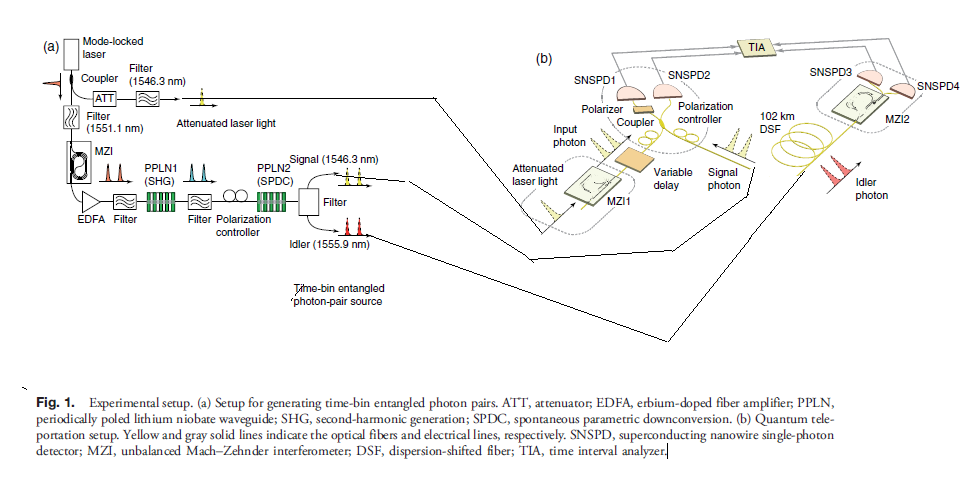
Рис. 1. Схема экспериментальной установки. (А) Установка для генерации временем бин запутанных пар фотонов. ATT, аттенюатора; EDFA, эрбиевый волоконный усилитель; PPLN, регулярной доменной ниобата лития волновод; SHG, генерация второй гармоники; ГСМР, спонтанное параметрическое рассеяние. (Б) Установка для квантовой телепортации. Желтые и серые сплошные линии обозначают оптические волокна и электрических линий, соответственно. SNSPD - сверхпроводящий из нанопроволоки однофотонный детектор; MZI - несбалансированный интерферометр Маха-Цандера; DSF - (с  дисперсионной коррекцией) оптическое волокно  ; TIA-  анализатор временного интервала.

 

Работа по сигнальным фотонам [22]. Мы удалили передающего волокна и ИМЦ, а холостые фотоны были непосредственно получены SNSPD3. Weobserved theHOMinterference приняв тройных совпадений между SNSPD1, SNSPD2 и SNSPD3 как функции относительная задержка между входным и сигнальных фотонов. Заметим, что этот эксперимент соответствует квантовой интерференции между ослабленным лазерным импульсом и возвестил один фотон, и теоретический предел видимости приближается к 100%, когда среднее количество входных фотонов в импульсе уменьшается и, когда фоновые значения детекторов незначительны [23]. Результат показана на рис. 2 (а). При нулевой относительной задержки, мы наблюдали четкое падение в тройках.

 

Рисунок 1 (а) показывает конфигурацию временной бункера запутанными фотон источником пара. Субпикосекундных импульсы от волокна modelocked лазер с частотой повторения 35.53 МГц пропускают через волны фильтра, центр которой длина волны и пропускная способность являются 1551.1 нм, и 20 ГГц, соответственно. Как Результат, мы получаем импульсы с временной ширины ~ 20 пс.

Импульсы запущен в неуравновешенное Маха-Цандера интерферометра (ИМЦ), чьи временная задержка 1 нс, чтобы создать двойные импульсы. 

 Двойные импульсы усиливаются эрбиевого волокна усилитель и запущен в первом РДС лития ниобата (PPLN) волновод, в котором последовательность импульсов насоса с длина волны 775,6 нм генерируется с помощью второй гармоники Процесс генерации. В 775,6 нм импульсы затем пропускают через фильтр для устранения 1551,1 нм свет и вводятся во второй PPLN волновода, где время-бен запутываются пары фотонов, чьи состояние задается jψi? ? J1is j1ii? j2isj2ii? / ffiffiffi р2 генерируются через спонтанного параметрического процесса преобразования с понижением частоты.

Здесь jxiy обозначает состояние, при котором существует фотон при временном слоте х в режиме у.

Сформированные пары фотонов делятся на сигнал (1546,3 нм) и промежуточная (1555,9 нм) каналов с использованием длины волны фильтр с полосой пропускания передачи 20 ГГц для обоих Каналы, в результате чего фотон пары времени когерентности ~ 20 пс. Чтобы приготовить входной кубит, длина волны которого такой же, как фотона сигнала, часть выходе из волокна modelocked лазерная (до спектральной фильтрации) извлекается с помощью 99: 1 волокна переходник, прошло через аттенюатор, чтобы сделать среднюю фотон Количество в импульсе много меньше 1, а затем выведен на оптический полосовой фильтр, длина волны которого и передачи пропускная точно такие же, как те, которые используются для разделения сигнала фотоны. Выход ослабляется лазерный импульс подается на вход другого несбалансированное интерферометр (MZI1) которого временная задержка 1 нс создать времени бин кубит для использования в качестве входного фотона. Наша несбалансированным интерферометры основаны на силикагеле, волновода. фаза Различия между двумя волноводно оружия стабильно контролируется настраивая температуру волновода [19].

В следующем телепортации Эксперимент, мы устанавливаем среднее число фотонов в кубит для запутанных пар фотонов и входных фотонов на 0,016. Характеристики запутанном пары фотонов времени бин Источник описаны в Приложении 1.

Установка для нашей квантовой телепортации эксперимента показан на фиг. 1 (б). Фотоны сигнальные и входные пропускают через Контроллеры поляризации, а затем пустился в дБ волокна 3 переходник с последующим SNSPD1 и SNSPD2. Здесь, временная различимость между двумя фотонами устраняется регулируя временное положение входных фотонов с использованием Переменная линия задержки, а поляризация различимость является устранены путем корректировки контроллеры поляризации, чтобы максимизировать число фотонов, которые прошли через поляризатор помещают в фронт SNSPD1. Мы можем спроектировать два фотона в jΨ-I от Кондиционирование о событиях, где оба SNSPD1 и SNSPD2 обнаружения фотоны, но в разных временных интервалах, как описано в Приложении 1. Холостой фотон передается через 102 км со смещенной дисперсией волокна, и получен другой несбалансированного интерферометра (MZI2), чьи два выходных порта подключены к SNSPD3 и SNSPD4.

Потери в оптическом волокне длиной  102 км  составляли 21,8 дБ, в том числе потери в разъемах. Следует отметить, что 102 км волокна наматывали на катушки и было физическое разделение между временем бин запутывания источник и MZI2 был в нескольких метрах. Благодаря узкой пропускная способность холостого фотона, временная форма сигнала расширения связанное с дисперсией высокого порядка в волокне пренебрежимо мала. Сигналы обнаружения от SNSPDs принимаютс времени Интервал анализатор (TIA) для измерений совпадений. По кондиционирования события обнаружения в SNSPD3 или SNSPD4 на успешное проекция сигнала и входных фотонов jΨ-I, мы можем телепортировать квантовое состояние входного фотона, что и бездельника Фотон с заданной унитарного преобразования.

 

Следует отметить, что мы можем реализовать два неортогональных измерения, использующие MZI2 последующим двух детекторов одиночных фотонов [20,21]. Обозначим разность фаз между двумя Руки MZI2 по в2. Когда времени бин кубит проходит через MZI2, детекторы могут, возможно, обнаружить фотон в трех времени слоты. Обнаружения фотона во втором временном интервале с SNSPD3 и SNSPD4 означает, что входной кубит прогнозируется состояниям? j1i? eiθ2 j2i? / ffiffiffi P2 и j1i -? eiθ2 j2i / ffiffiffi р2, соответственно.

С другой стороны, когда мы зафиксировать фотон в первом или третий слоты времени с любой из детекторов, кубит прогнозируется государственной j1i или j2i соответственно. Далее мы относиться к Измерение проекции на второй слот как superpositionbasis Измерение, и что на первой или третьей прорези как Время-основы измерения. Эффективность регистрации системы SNSPDs были 80% (SNSPD1), 86% (SNSPD2 и SNSPD3), и 81% (SNSPD4), в то время как фоновые скорости счета были ~102 гц для всех детекторов. Джиттер из SNSPDS был ~ 90 пс, и, таким образом погрешности измерений, вызванные межсимвольной интерференции были незначительным в нашем эксперименте, где временная разница между временем бункеров был 1 нс. В SNSPDs подробно описаны в Приложении 1.

Мы провели-НУ-Mandel Хонг (НОМ) помехи Эксперимент, чтобы исследовать неразличимости входе и (Б) Фильтр PPLN1 (SHG) EDFA Режим автоподстройки лазер поляризация контроллер PPLN2 (ГСМР) ИМЦ Фильтр (1551,1 нм) Фильтр Фильтр Сигнал (1546,3 нм) Холостой (1555,9 нм) ATT Фильтр (1546,3 нм)

 

Видимость HOM провала был 76,9? 3,4%, что значительно превысило классический предел видимости HOM 50%. Поскольку ширина импульса накачки и времени когерентности фотонные пары были похожи в нашем эксперименте, оставшиеся частоты Корреляция между запутанных фотонов ожидается чтобы быть основным источником сокращения видимости от 100%. Затем мы провели квантовую телепортацию эксперимент.

Мы сначала удаляют волокна передачи от установки, показанной на Инжир. 1.We запущенные входные фотоны, чье состояние определяется? J1i? eiθ1 j2i? ffiffiffi р2, установив фазу MZI1 на б1 и наблюдается События обнаружения фотонов с SNSPD3 и SNSPD4 В разделе базисе по суперпозиции кондиционером на проекции сигнала и входные фотонов jΨ-I. Результат показан на фиг. 2 (а) (SNSPD3) и 2 (б) (SNSPD4).

Таким образом, мы подтвердили, что фаза входного фотона была успешно передана, что холостой фотон. В заметность были 60,5? 5,0% для Канал SNSPD3 и 57,5? 5,7% для канала SNSPD4. Обратите внимание, что мы не вычитаем любые случайные совпадения или фон рассчитывает любой из экспериментальных данных показано В этом письме. В этом эксперименте, индуцированной ограниченной видимости ХОМ ошибки в государственном измерении Bell, в результате чего ухудшение видимости полос от 100%.

Затем мы провели квантовую телепортацию эксперимент над 100 км волокна для шести различных входных состояний. Мы подготовили состояния J? я? ? J1i? j2i? / ffiffiffi р2, JLI? ? J1i? ij2i? / ffiffiffi p2 и ИСР? ? J1i -? Ij2i / ffiffiffi р2, регулируя фазовое б1 MZI1, а другая двух государств j1i и j2i были получены путем удаления MZI1 и корректировки временные позиции кубитов, так что они совпадали с, что из первого и второго импульсов фотонов сигнальных, соответственно.

Обратите внимание, что в нашем эксперименте квантовой телепортации, входные состояния фотона j1i, j2i, JLI, ИСР, и J? я преобразуются к бездельника состояния фотона j2i, j1i, JLI, ИСР и J? I, соответственно

(См Приложение 1 для более подробной информации). Мы провели квантовое состояние томография (QST) [24] на телепортируемом государств, чтобы получить их матрицы плотности. Мы использовали шесть измерений проекции, что соответствуют J? я, JLI, Ri, j1i, и j2i выполнять QST на одного кубита.

Прогнозы на J? Я и J-я были достигнуты выполняя суперпозицию базисных-измерения с в2? 0 на SNSPD3 и SNSPD4, соответственно, в то время как прогнозы JLI и ИСР были осуществляться с использованием суперпозиции-базис Измерения при SNSPD3 и SNSPD4, соответственно, с θ2? π / 2.

Прогнозы на j1i и j2i были достигнуты с Время-основы измерения на первом и третьем временных интервалах, соответственно. Так как наша установка была изначально оснащен двумя неортогональных методы оценки, мы могли бы выполнить шесть выступов только с двумя измерениями TIA на в2? f0; π / 2g [21]. Время сбора данных для каждого измерения TIA 6000 с,

Это означает, что общее время измерений QST для каждого входа состояние было 12000 с. Среднее число тройных совпадений для каждая базисная был ~170. С необработанные данные, полученные в ТПЗ Измерения, мы провели максимального правдоподобия для получения физически законные матрицы [24]. реконструирован матрицы плотности после максимального правдоподобия являются предусмотрено в Приложении 1.

Используя эти матрицы плотности, мы рассчитывается верность для каждого входного состояния. Результаты показаны на фиг. 3.

Мы получили среднюю верность 83,7? 2,0% для шесть различных входных состояний, что означает, что мы наблюдали нарушение классического предела (66,7%) более чем на восемь стандартных отклонения.

Если мы предположим, что состояние телепортируемом фотона является Вернер состояние, верность F и видимость бахрома V связаны а F? ? 1? V & beta; / 2. Это означает, что точность телепортации без 100 км волокна в показанной на фиг. 2 (б) и 2 (с) ~ 80%.

Таким образом, мы не наблюдали ухудшения верности, вызванную 100 км волоконно-передачи холостых фотонов, благодаря низкие шумовые характеристики в SNSPDs. В квантовой телепортации эксперимента над 100 км волокна в, мы наблюдали значительное смещение в Временное положение телепортированы фотоны, обусловлена ​​длины волокна флуктуации индуцированный изменений в комнатной температуре.

Поэтому мы реализованы структуры по контролю за дрейфа для стабильного подсчета тройных совпадений (см Приложение 1 для более подробной информации). Мы добились квантовой телепортации расстояние аналогичную тем, которые достигаются в предыдущих опытов, проведенных на свободном пространстве Каналы [12,13].

 

 

Рис. 2. Экспериментальные результаты для (а) помех HOM и (б), (в) квантовой телепортации без передающего волокна. (Б) и (в) соответствуют число тройных совпадений в течении периода в 120 с в зависимости от фазы  MZI1 наблюдаемого SNSPD3 и SNSPD4 соответственно.

 

В этих экспериментах, квантовые состояния из объявленные одиночные фотоны были телепортированы, который требуется в четыре раза измерения совпадений, а не тройной совпадение измерения требовали в нашем эксперименте.

Кроме того,  потери в оптическом канале (в том числе потери в оптике) в экспериментах, описываемых в работах [12,13] составляли на 10 дБ больше, чем в нашем эксперименте. Эти результаты показывают, что наш эксперимент по квантовой телепортации  менее эффективнее, чем те, в [12,13].

Это относительное неэффективность нашего эксперимента в основном определялась из-за неэффективного сопряжения фотонной пары с оптическим волокном (эффективность ввода излучения в оптоволокно составляла ~ 13%), которое было вызвано узкополосной фильтрацией частотно коррелированных фотонов. Оптические потери  в нашей установке при "тройной скорости совпадений" нашего эксперимента подробно описаны в Приложении 1.

Таким образом, мы показали, квантовую телепортацию фотонной кубита более 100 км оптического волокна.

Этот результат подтвердил осуществимость дальней квантовой связи на основе квантовой телепортации по оптическому волокну. К тому же, мы можем ожидать, что высокоэффективные многократные измерения  фотонов с использованием фотодетекторов SNSPDs проложит путь к передовым квантовым системам связи, основанным на генерации многофотонных квантовых состояниях таких, как  состояния фотонов Гринбергер-Хорн-Цайлингер [25] и многофотонные и кластерные состояния  [26], и передачи  по оптическому волокну.

REFERENCES

1. N. Gisin and R. Thew, Nat. Photonics 1, 165 (2007).

2. H. K. Lo, M. Curty, and K. Tamaki, Nat. Photonics 8, 595 (2014).

3. C. Gobby, Z. L. Yuan, and A. J. Shields, Appl. Phys. Lett. 84, 3762 (2004).

4. H. Takesue, S. W. Nam, Q. Zhang, R. H. Hadfield, T. Honjo, K. Tamaki, and Y. Yamamoto, Nat. Photonics 1, 343 (2007).

5. B. Korzh, C. C. W. Lim, R. Houlmann, N. Gisin, M. J. Li, D. Nolan, B. Sanguinetti, R. Thew, and H. Zbinden, Nat. Photonics 9, 163 (2015).

6. T. Honjo, S. W. Nam, H. Takesue, Q. Zhang, H. Kamada, Y. Nishida, O. Tadanaga, M. Asobe, B. Baek, R. Hadfield, S. Miki, M. Fujiwara, M. Sasaki, Z. Wang, K. Inoue, and Y. Yamamoto, Opt. Express 16, 19118 (2008).

7. H. J. Briegel, W. Dur, J. I. Cirac, and P. Zoller, Phys. Rev. Lett. 81, 5932 (1998).

8. N. Sangouard, C. Simon, H. de Riedmatten, and N. Gisin, Rev. Mod. Phys. 83, 33 (2011).

9. C. H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, and W. K. Wootters, Phys. Rev. Lett. 70, 1895 (1993).

10. D. Bouwmeester, J. W. Pan, K. Mattle, M. Eibl, H. Weinfurter, and A. Zeilinger, Nature 390, 575 (1997).

11. A. Furusawa, J. L. Sorensen, S. L. Braunstein, C. A. Fuchs, H. J. Kimble, and E. S. Polzik, Science 282, 706 (1998).

12. J. Yin, J.-G. Ren, H. Lu, Y. Cao, H.-L. Yong, Y.-P. Wu, C. Liu, S.-K. Liao, F. Zhou, Y. Jiang, X.-D. Cai, P. Xu, G.-S. Pan, J.-J. Jia, Y.-M. Huang, H. Yin, J.-Y. Wang, Y.-A. Chen, C.-Z. Peng, and J.-W. Pan, Nature 488, 185 (2012).

13. X.-S. Ma, T. Herbst, T. Scheidl, D. Wang, S. Kropatschek, W. Naylor, B. Wittmann, A. Mech, J. Kofler, E. Anisimova, V. Makarov, T. Jennewein, R. Ursin, and A. Zeilinger, Nature 489, 269 (2012).

14. I. Marcikic, H. de Riedmatten, W. Tittel, H. Zbinden, and N. Gisin, Nature 421, 509 (2003).

15. F. Bussieres, C. Clausen, A. Tiranov, B. Korzh, V. B. Verma, S. W. Nam, F. Marsili, A. Ferrier, P. Goldner, H. Herrmann, C. Silberhorn, W. Sohler, M. Afzelius, and N. Gisin, Nat. Photonics 8, 775 (2014).

16. F. Marsili, V. B. Verma, J. A. Stern, S. Harrington, A. E. Lita, T. Gerrits, I. Vayshenker, B. Baek, M. D. Shaw, R. P. Mirin, and S. W. Nam, Nat. Photonics 7, 210 (2013).

17. V. B. Verma, B. Korzh, F. Bussieres, R. D. Horansky, S. D. Dyer, A. E. Lita, I. Vayshenker, F. Marsili, M. D. Shaw, H. Zbinden, R. P. Mirin, and S. W. Nam, “High-efficiency superconducting nanowire single-photon detectors fabricated from MoSi thin-films,” arXiv:1504.02793 (2015).

18. J. Brendel, N. Gisin, W. Tittel, and H. Zbinden, Phys. Rev. Lett. 82, 2594 (1999).

19. T. Honjo, K. Inoue, and H. Takahashi, Opt. Lett. 29, 2797 (2004).

20. W. Tittel, J. Brendel, H. Zbinden, and N. Gisin, Phys. Rev. Lett. 84, 4737 (2000).

21. H. Takesue and Y. Noguchi, Opt. Express 17, 10976 (2009). 22. C. K. Hong, Z. Y. Ou, and L. Mandel, Phys. Rev. Lett. 59, 2044 (1987).

23. J. G. Rarity, P. R. Tapster, and R. Loudon, J. Opt. B 7, S171 (2005).

24. D. F. V. James, P. G. Kwiat, W. J. Munro, and A. White, Phys. Rev. A 64, 052312 (2001).

25. J. W. Pan, D. Bouwmeester, M. Daniell, W. Weinfurter, and A. Zeilinger, Nature 403, 515 (2000).

26. P. Walther, K. J. Resch, T. Rudolph, E. Schenck, H. Weinfurter, V.