Времени подобные области пространства и времени ("время подобно"), позволяющие путешествовать в прошлое.  

Traversable Achronal Retrograde Domains In Spacetime, 2013

Doctor Benjamin K. Tippett ,Gallifrey Polytechnic Institute ,Doctor David Tsang Gallifrey Institute of Technology (GalTech)

 

 Есть много пространственно-временные геометрических метрик  в общей теории относительности, которые содержат замкнутые времени подобные кривые.  Можно сказать, что  время в пути можно таким пространства-времени. На сегодняшний день никто не обнаружил пространство- геометрия которого эмулирует (изменяется), и  которое можно  описать, как пространство, в котором выполняются условия для существовании  машины времени.

Цель данной работы заключается в предложить такую геометрию пространства-времени. В нашей геометрии, замкнутый объем кривизны перемещается вдоль замкнутой траектории. Внутри этого объема существует Риндлер пространство, а его  внешняя  оболочка есть пространство-время Минковского. Ускорение наблюдателей внутри таких объемов позволяет совершать  путешествия в прошлое, как на машине времени , вдоль замкнутых  времени подобных кривых. Стены такого объема(пузыря) генерируются с вопроса, который нарушает классическую энергию условия. Мы имеем в виду такой пузырь в качестве TRAVERSABLE Achronal ретроградной Домены в пространстве-времени "время подобно".

 

 

ВВЕДЕНИЕ

A. Экзотические хронотопы

Как  можно сконструировать или построить машину времени "время подобно"? Начнем с рассмотрением именно того, что может означать, что такое есть "Машина времени"? Герберт Уэллс (и его преемники) описали такой аппарат, который мог бы перенести людей "назад в прошлое время". То есть, перенести их из текущей точки места в пространстве-времени в точку  собственного причинного прошлого. Если мы опишем время как поток,  с течением времени, как наш безжалостный поток вдоль наших коллективных мировых линий по отношению к нашего будущего; то  машина времени будет позволять проводить нас вверх по течению - то есть назад в прошлое. Позвольте нам описать такие движения, как путешествие в прошлое время.

В контексте общей теории относительности, как в реке, это лежащая в основе геометрии который определяет, где мировые линии может протекать. В общем, это возможно для пространственно-временной геометрии разрешить ретроградной путешествие во времени [13]. При обсуждении причинность, мы часто описывают геометрию с точки зрения ориентации световых конусов. Световой конус "время подобно"новых с определенной точки может служить для разграничения точки которые могут и не может быть достигнуто с этой точки вдоль времени подобных траектории.

В геометрии, которые позволяют  путешествие в прошлое есть регионы, где  световые конусы чаевые в пути, который позволяет нашим времени подобные мировые линии разлива назад к "прошлому". В таких областях пространства-времени  возможно существование замкнутых  времени подобных кривых, которые замыкаются на себя -подобно  змее, пытающейся съесть ее хвост. Такие кривые называются  замкнутыми времени- кривых (КТК). Наличие КТК в пространстве-времени используется для разграничения их на хронотопы, где возможно обратить время в прошлое или назад. ЦОК чаще всего генерируется в результате момент в пространстве-времени"время подобно". Первый геометрию быть обнаружено у КТК предполагает решение космологической генерируется путем поворота пыль [7]. Пространство-Керр и Tomimatsu-Сато хронотопы [21] содержат CTCs в их интерьере регионы. ЦОК могут быть получены в пространстве  бесконечно длинного  вращающегося цилиндра вещества [22], (известный как цилиндров Типлер) [20].

Кроме того, существует теория существования пространства , как двух космических струн вложенных одной в другую, данная теория космических струн также подтверждает существование ( или генерацию) СТС [9], [2].

T Икс В

Рисунок 1: Схема пространства  пузыря-объема ТАРДИС "время подобно". Стрелки обозначают  направление времени. Соратники Эми (А) и Барбара (Б) находятся в различных областях пространства - внутри и снаружи пузыря ТАРДИС. Внутри  ТАРДИС пузыря  существуют замкнутые времени подобные кривые, и  временная координата для наблюдателя А замкнута, и она А перемещается с ростом времени по  круговой траектории. Вне пузыря, наблюдатель видит Б время последовательно увеличивается в вертикальном направлении"время подобно". Жизнь внутри пузыря красочна и весела. Жизнь за пределами пузыря серая и однообразная, и платье на Б, как на школьном учителе  1960-х годов.

Возможны существование или генерации CTCs в  метриках, которые  преднамеренно содержат CTCs. Ори [17] и Ори-Сон [16] исследовали область пространства-времени в  телесности и обнаружили область"время подобно", в которой генерируются CTC. Если взять две проходимой червоточины(кротовые норы)  правильно ускорен относительно на один другой, парадокс близнецов может привести к пути между CTC входные отверстия [3, 6].

Наконец, хронотопы, где кривые времени подобные могут путешествовать вместе сверхсветовых (как описано удаленным наблюдателем) траектории  2 (а) границы ТАРДИС в Т = 0 границы (б) TARDIS в Т =? 50 Границы (C) TARDIS в Т =? 75 границы (г) TARDIS в Т =? 100

Рисунок 2: Эволюция границ пузыря, а определены в разделе II А, как видно по внешнему наблюдателю. В Т = ??100 пузырь внезапно появляются, и раскол в до двух штук, которые будут двигаться друг от друга (Т = 75; Т = 50). При Т = 0, два пузырьки придет к отдохнуть, а затем начать ускорение в направлении одной другой (Т = +75; Т = + 50). После чего, при Т = +100 два пузырьки "время подобно" сольются и исчезнут.

может быть использован для создания замкнутых кривых времениподобные. Алькубьерре основы привод [1] может быть использован для создания CTCs [4], [8]; в виде может ли Красников трубки [5], [12].

Если есть так много способов, чтобы идти об этом, почему не у нас никогда видел доказательства ретроградной время поездки в нашей Вселенной? Ответ зависит от конкретного СТС-содержащего геометрии.

Хронотопы "время подобно" позволяющие сверхсветовой путешествие часто требуют нарушение из классических энергетических условиях [13], [15], и Поэтому не классически реализуемы. Регион СТС в Керр пространство скрывается за горизонтом событий, в Tomimatsu- Сато геометрии не признаются в качестве endstate гравитационного разрушаться, и другие упомянутые модели требуют бесконечно большие распределения материи. Кроме того, существует аргумент, из-за Хоукингом [10], Известно, как гипотеза защиты хронология. Хокинга аргументы вокруг как большинство пространства-времени, которые идут от отсутствия CTC на ранней стадии, чтобы их обладающий более позднее время, также обладают компактно порожденная Коши горизонты. Он утверждает, что плотность энергии в пространстве-времени "время подобно"реалистичной будут расходиться непосредственно перед формированием ЦОК вдоль этих поверхностей (таким образом, искажающих геометрию, и, препятствующих их формирование) [10].

Несмотря на это зверинец CTC геометрий, мирянин может спросить ли какие-либо из этих решений может быть описана как на часто мечтал, машина времени? Конечно, ретроградная время путешествия можно во всех этих геометрий. С другой стороны, Типлер цилиндра [20] обнажает столько подобие в коробке, которая путешествует назад во времени, как лавина напоминает снег мобильный телефон.

Цель данной работы заключается в представлении геометрия пространства-времени которые мы могли бы просто описать как ящик, который путешествует взад и вперед вдоль контура в пространстве-времени. Аналогичный на диске Алькубьерре, это пузырь изогнутой геометрии встроен в замкнутом пространстве (flat), Минковского в вакууме. В отличие от Алькубиерре езды, траектория нашего пузыря закрыт в пространстве-времени.

В. Traversable Achronal ретроградная домена Наша пространство "время подобно" содержит пузырь геометрии, который распространяется вдоль закрытого (круговой) путь через Минковского. Ускорение наблюдателей в пузырь может путешествовать по времени- кривых, которые закрывают в worldtube пузыря. An наблюдатели Путешествия в пузырь будет рассказать резко ди? различны история из наблюдателей за его пределами.

Проиллюстрировать общие свойства этого пространства-времени, давайте представим себе, пару товарищей: одна по имени Эми (А), который едет в пределах пузырь; а другой с именем Барбара (В), который оставил и остается за его пределами. Давайте также, что стены пузыря являются прозрачными, и оба наблюдатели проведения вверх большие часы (см. 1).

Как Эми описывает траекторию ее пузыря? Против часовой стрелки в пространстве-времени! Первоначально, она начинает двигаться в досветовом Скорость влево (вперед развивается во времени по отношению к внешности Минковского). Пузырь затем начинает ускоряться до тех пор, пока движется со сверхсветовой скоростью в (развернуться в время).

Пузырь затем замедляется до досветовых скоростях, но Теперь он движется в обратном направлении по отношению к времени Минковского внешний вид. Наконец, она начинает ускорить вправо ( к его начальное положение), пока не будет снова движется со сверхсветовой, после чего замедляется и его worldtube закрывается. Эми увидите руки своей тактовой ходу часовой стрелки всей время. Когда она смотрит на часы Барбары, она увидит это поочередно двигаясь по часовой стрелке и против часовой стрелки двигаться. Барбара, глядя на Эми, увидите что-то довольно своеобразный. В какой-то начальный момент времени (T = ??100 на рис. 2), два пузыря вдруг появляются, двигаясь от одного-другого. Два пузырьки "время подобно"будет замедляться, останавливаться (при Т = 0), а затем начать движение обратно к друг другу, пока они не сливаются (при Т = +100).

Amy появится в обоих пузырьков: The Стрелки часов "время подобно" будут вращаться по часовой стрелке в одном пузыре, и против часовой стрелки в другом.

Обратите внимание, что интерпретация Барбары событий не в отличие от что используется для описания пара-создание и последующее уничтожение пары позитрон-электрон: мы часто описывают позитронно как электрон, который движется в обратном направлении в время.

3 Из-за уникальных особенностей этой геометрии пузырька, мы имеем в виду к нему как к Traversable Achronal ретроградного домена в пространстве-времени (ТАРДИС), и мы будем исходить, чтобы описать его геометрию ниже.

II. ТАРДИС ГЕОМЕТРИЯ

А. Метрическая Геометрия ТАРДИС -"время подобно" имеет метрику:

ds 2 = " 1 ?? ч (х; у; г; т)   2t2 x2 + t2 #! (??dt2 + dx2) + H (X, Y, Z; т)   4xt x2 + t2 ! dxdt 2 + dy + dz2 (1)

Подобно пузыря Алькубьерре, этот показатель опирается на TopHat Функция Н (х; у; г; т) для демаркации границы между внутри пузыря ч (х, у, г; т) = 1 и внешней пространства-времени ч (х; у; г; т) = 0.

Очевидно, на внешней стороне пузырька (где Н (х; у; г; т) = 0), эта метрика Минковского пространство. Рассмотрим геометрию, которая является наблюдателем внутри пузырь будет видеть. В этом регионе: H (X, Y, Z; т) = 1, и метрика может быть переписан:

ds 2 =   х2 ?? T2 x2 + t2 ! (??dt2 + dx2) +   4xt x2 + t2 ! dxdt 2 + dy + dz2 (2)

которые, в соответствии с преобразованием координат:

т =? грех (?); х =? COS (?)

становится Риндлер пространство.

ds 2 = ??? 2d? 2 + d? 2 + dy 2 + dz2 (3)

Геометрия Риндлер в этом контексте имеет модифицированную топология, составив выявления поверхностей? = 0 ? = 2 ?. Таким образом, траектории описывается постоянным? знак равно

; Y

знак равно Y ;

г = Z координаты будут закрыты времениподобная -"время подобно" кривых.

Следует отметить, что в то время как такие кривые не геодезической, ускорение требуется, чтобы остаться на этой траектории может быть скромным. Если Ла = [1

? ; 0; 0; 0] обозначает вектор касательной к одной из этих КТК, и Ка = [0; 1; 0; 0] ортогональный вектор пространственноподобная:

KaLbrbLa = 1 :

Наблюдатель движется вдоль одной из этих кривых "время подобно"будет чувствовать ускорение равно 1 = A. Таким образом, чем шире "Радиус" из траектория пузырька в пространстве-времени, тем слабее ускорение необходимое для перемещения вдоль ЦОК в нем.

Определим край пузыря ТАРДИС иметь Форма квадратная с шаровидным (с радиальным параметра R) движется вдоль круг радиуса "" А в х ?? т плоскости (рис 2).: ч (х; у; г; т) = Н ? R4 ?? Z4 ?? у4 ?? час x2 + t2 ?? А2 i2? (4)

где Н (х) обозначает функцию Хевисайда. Мы будем аппроксимировать функцию Хевисайда, используя непрерывный Функция Тань:

Н (х) = 1 2 + TANH (? х) 2 : (5) ?

параметр может быть установлен для определения внезапности Переход между внутренней и внешней стороне пузырька.

Все модели построены численные в этой статье будет указывать А = 100, R = 70 и? = 1 6000000.

Б. Причинная структуры  -"время подобно"

Для того, чтобы исследовать причинную структуру пузыря ТАРДИС Геометрия (время подобно), на рис. 3 имеем Ray-прослеживается нулевые геодезические по среза у = 0, г = 0. Пересечение любых двух нулевые геодезические, показывают, как световые конусы наклонены. Вдоль ось х (т = 0), все световые конусы указаны вверх-вниз.

Заметка что, как мы движемся вдоль внутренней пузыря, световые конусы наконечник соответствующим образом, чтобы круговым траекториям КТК. Интересно, что наблюдатель в пузырь смогут см прошлое (или будущее) версии самих себя Путешествия в пузырь.

Нулевые геодезические, когда они сталкиваются стены пузыря, может ди? RACT сильно. В результате некоторые из нулевых кривых будет е? ectively "обернулся время" (см. 4). Таким образом, в то время некоторые из геодезических на рис. 3 имеют конечные точки на будущее и мимо пустой бесконечности (синего цвета), другие имеют конечные только в будущем нулевой бесконечности (красный), или только в прошлом нулевой бесконечности (зеленый).

Это иллюстрирует тот факт, что ни пространство, не содержащий пузырь ТАРДИС может быть глобально гиперболической, и что пузырь должен быть источником горизонта Коши.

Рассмотрим схему на рис. 4, которая иллюстрирует это различные поведения "время подобно". Красные кривые являются те, которые происходят из прошлого нулевой бесконечности и либо пропустить пузырь или ди? RACT через него, а затем заканчивается в будущем нулевой бесконечности. красные кривые получить сильно ди? racted в пузыре, и обе конечные точки лежал на будущей нулевой бесконечности. Из этих кривых, геодезические которые связаны этот набор (в черном) среди тех геодезических которые генерируют горизонт Коши. Они самые ранние нулевые геодезические выйти из пузыря. Отметим, что эти геодезические не компактно порождена, и мы считаем, что Защита хронология гипотеза Хокинга не будут применяться к это пространство [10, 11].

В заключение отметим, что, в центре семейства нуль кривые, которые были сложены в пространстве-времени над (рис. 4), должен быть один нуль кривой, которая будет сложена на себя, и, следовательно, не может быть продлен до произвольной параметрической длина. Это не ясно, следует ли интерпретировать это конечная точка как особенность. Мы не обнаружили какой-либо расходящегося Поведение в геометрии в непосредственной близости от этой точки.

С. Напряженность тензора энергии

Чтобы дать представление о материи, необходимой для перехода между интерьер и наружные пылесосы пузырька, у нас есть 4

Рисунок 3: Нулевые геодезические, проходящие через поперечное сечение Y = 0; Z = 0. Черные кружки представляют края пузыря. Зеленый Кривые будут отражаться по геометрии пузыря и не будет пересекать любые гиперповерхности Пространственноподобные, которые лежат далеко в будущее из пузырь. Красные кривые также отражено, и не будет пересекать любые пространственноподобные гиперповерхности, которые лежат далеко в прошлое пузыря.

Синие кривые пересекутся как будущее и прошлое пространственноподобные гиперповерхности "время подобно". Обратите также внимание, световые конусы в пределах наклона, чтобы позволить пузыря времениподобные наблюдатели путешествовать по замкнутым круговым, мировых линий. нанесены различные ненулевые компоненты энергии напряжений Тензор принято по сечениям геометрии пространства-времени.

Последовательно, классические энергетические условия нарушаются.

Если мы положим Y = 0; Z = 0, мы видим поперечное сечение пузырька как он перемещается вдоль круговой конечно через пространства-времени. только ненулевые элементы тензора энергии-импульса вдоль этого срез являются ненулевыми давление в у и г направлениях, как видно на рис. 5a и 5b соответственно.

Если мы положим Y = 0; т = 0, мы видим поперечное сечение пузырька (ы) в состоянии покоя по отношению к внешней системе координат. Там отличны от нуля давление, а также сдвиг термины, как видно на рис. 6а, 6b и 6c.

Если мы положим т = 0; х = 100, мы видим поперечное сечение пузырь на плоскости уг"время подобно", когда пузырь в состоянии покоя относительно внешний системе координат. В этом случае единственный ненулевой элементы тензора энергии-импульса вдоль этого кусочка являются сдвига Термины, как показано на фиг. 7a и 7b. Плотность энергии не равно нулю во всем мире. Если мы посмотрим на сечения, которые не лежат на х ?? т ось (поперек ломтик г = 30; у = 0 на рис. 8), мы видим, более сложный тензор энергии-импульса.

III. Обсуждение

Проблемы с ТАРДИС Metric  -"время подобно"

Наша метрика (Eq.1) симметрична перемены знака из координата времени или X, Y, Z координаты. Как следствие, наблюдатели могут путешествовать по всему ЦОК на рис. 3 в любом часовой стрелке или против часовой стрелки.

Световые конусы, которые лежат на границе пузырька, и переход гладко между ориентацией внутри пузыря и ориентация пределами пузыря, не может пребывать

5 Коши Горизонт Заканчивается в особенность

Я + I ±

Рисунок 4: Схематическое изображение -"время подобно"из набора кривых параллельных нулевых преломляясь краями подвижной пузыря. Пунктирная линии представляют стены пузыря. Черный кривая является генерации кривой горизонт Коши. J? находятся сокращение для будущего и прошлого нуль нуль бесконечности, соответственно. эта симметрия. Например, если общая метрика симметрична при переключении знак Х-координата, есть нет уникален и соответствует способ для световые конусы, чтобы склонить чашу на указывает, где стены пузырь пересекаются в точках х = 0. Более широкое проявление этого вопроса является то, что есть моменты, где оба GTT = Gxx = 0 и GTX = GXT = 0.

Вопрос можно решить, разбив эту симметрию, и принятии решения стрелкой времени внутри и снаружи пузыря "время подобно".

Это может быть сделано путем добавления дополнительного срока для метрики, которые заставляет световые конусы на границе пузыря крутить в преднамеренное путь:

ds 2 = " 1 ?? ч (х; у; г; т)   2t2 x2 + t2 #! (??dt2 + dx2) + H (X, Y, Z; т)   4xt x2 + t2 ! dxdt 2 + dy + dz2 + 4t3h (х; у; г; т) W (х; у; г; т) dxdt (6) (а) Gzz по среза у = 0; г = 0 (б) Гыы вдоль среза у = 0; г = 0

Рисунок 5: ненулевых членов тензора энергии-импульса вдоль ломтик  -"время подобно"

у = 0; г = 0. где Вт (х; у; г; т) = 1 2   TANH ( х2 ?? T2 (2ч (х; у; г; т) ?? 1) + 20 T2) ?? TANH ( х2 ?? T2 (2ч (х; у; г; т) ?? 1) ?? 20 T2) ! : (7)

The W (х; у; г; т) функция служит для обеспечения GTX, 0 вообще точки, в которых GTT = Gxx = 0, а также, что дополнительный член 6 (а) Gzz по среза у = 0; т = 0 (б) Гыы вдоль среза у = 0; т = 0 (с) Gxz по среза у = 0; т = 0

Рисунок 6: ненулевых членов тензора энергии-импульса вдоль ломтик у = 0; т = 0 (а) Gxz вдоль кусочек т = 0; х = 100 (б) Gxy вдоль кусочек т = 0; х = 100 Рисунок 7: ненулевых членов тензора энергии-импульса вдоль ломтик х = 100; т = 0. исчезает, когда вы дальше от границы пузыря.

Путешествия между произвольными точками в пространстве-времени В то время как геометрия, как это предусмотрено в Eq.1 обладает CTCs, мы считают, что это только верхушка айсберга, когда дело доходит до с помощью этого геометрию как «машины времени». 7 (а) Gtt по ломтик г = 30; у = 0 (б) песчаный вдоль среза г = 30; у = 0 (в) Gxx вдоль среза г = 30; у = 0 (d) Gxz по ломтик г = 30; у = 0 (е) Гыы вдоль среза г = 30; у = 0 (е) Gzz по среза г = 30; у = 0

 

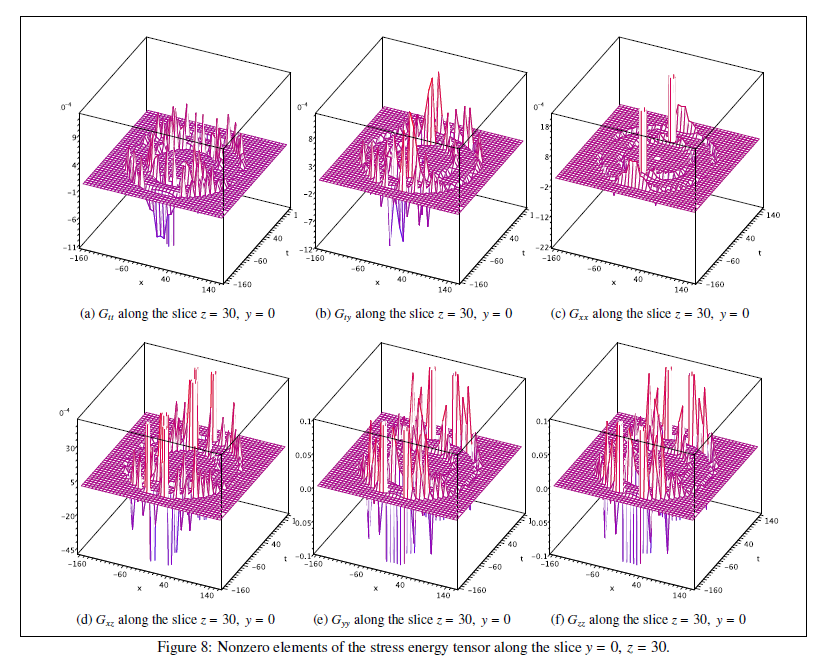
Рисунок 8: Ненулевые элементы тензора энергии-импульса вдоль среза у = 0; г = 30.

Используя условия Израиль-Дармуа распределительные [18], разделы ди? различны ТАРДИС пузырь траектории можно вырезать и затем сшиты вместе конца в конец. Как следствие, учитывая любые две точки пространства-времени Минковского, цепи ТАРДИС геометрии могут быть собраны таким образом, что поставить первый точка в причинном прошлом секунду.

Вопросы для дальнейшего рассмотрения

1. Квантовая теория поля: Мы можем предвидеть несколько интересных вопросы, касающиеся как квантованных полей будет вести себя в геометрии ТАРДИС.

-Suppose, Что Израиль-Дармуа условия сопряжения используется, чтобы плавно войти в верхнюю половину (т? 0) из ТАРДИС метрики нижней половине (т <0) Минковского метрики. Будет электрон, который поступает в пузырь от одна сторона появляться с другой стороны, как позитрон?

-Since Интерьер пузыря выглядит Риндлер пространство, будет наблюдатели путешествия в пузырь см Унру излучение?

-Since Это пространство обязательно имеет горизонт Коши, он будет обладать нестабильности типа масс-инфляция [19]? Будет некоторые из аргументов защиты хронологии гипотезу применить к нему? -Should Любой из нулевых 3-поверхностей, связанных это будет Геометрия быть описана как горизонтов событий? Если да, то любое излучение Хокинга быть связаны с ними?

2. Опасные Blueshifting: Алькубьерре основы пузырь который замедляет от траектории пространственноподобной к времяподобным Траектория было показано синее смещение излучения поймали на поверхности пузырьков [14]. Так ТАРДИС пузыри идет назад и вперед от того пространственноподобная и времениподобная, будет аналогичный процесс происходит?

3. Особенности не: Наша беглый расследование выявило нет кривизны особенности, и в стороне от обсуждаемых вопросов в Sec.III, метрика хорошо себя every8 где. Несмотря на это, как мы обсуждали в Sec.II B, это не неразумно ожидать, что это своеобразный причинного структура должна сопровождаться рода сингулярности.

Есть ли другие особенности этого пространства-времени в? Какова их природа?

Авторы

Мы хотели бы поблагодарить д-ра Чад камбуз и д-р Уильям Унру, для их содержательные дискуссии; и ZachWeinersmith за его замечания. Мы также хотели бы поблагодарить д-ра Джона Смит. 

 

[1] M. Alcubierre. The warp drive: Hyper-fast travel within general relativity. Class. Quantum. Grav., 11(L73-L77), 1994.

[2] S. Deserr, R. Jackiw, and ’t Hooft, G. Physical cosmic strings do not generate closed timelike curves. Phys. Rev. Lett., 68(3):267–269, 1992.

[3] F. Echeverria, G. Klinkhammer, and K. S. Thorne. Billiard balls in wormhole spacetimes with closed timelike curves: Classical theory. Phys. Rev. D, 44(4):1077–1099, 1991.

[4] A. E. Everett. Warp drive and causality. Phys. Rev., 53(12):7365–7368, 1996.

[5] A. E. Everett and T. A. Roman. Superluminal subway: The krasnikov tube. Phys. Rev. D, 56(4):2100–2108, 1997.

[6] J. Friedman, M. S. Morris, I. D. Novikov, F. Echeverria, G. Klinkhammer, K. S. Thorne, and U. Yurtsever. Cauchy problem in spacetimes with closed timelike curves. Phys. Rev. D, 42(6):1915–1930, 1990.

[7] K. Godel. An example of a new type of cosmological solution of einstein’s field equations of gravitation. Rev. Mod. Phys., 21(3):447–450, 1949.

[8] P. F. Gonzalez-Diaz. Warp drive space-time. Phys. Rev. D, 62(044005), 2000.

[9] J. R. Gott. Closed timelike curves produced by pairs of moving cosmic strings: Exact solutions. Phys. Rev. Lett., 66(9):1126– 1129, 1991.

[10] S. W. Hawking. Chronology protection conjecture. Phys. Rev. D, 46(2):603–610, 1991.

[11] SW. Kim and K. S. Thorne. Do vacuum fluctuations prevent the creation of closed timelike curves. Phys. Rev. D, 43(12):3929– 3947, 1991.

[12] S. V. Krasnikov. Hyperfast travel in general relativity. Phys. Rev. D, 57(8):4760–4766, 1998.

[13] F. S. N. Lobo. Closed timelike curves and causality violation. arXif:1008.1127v1.

[14] B. McMonigal, G. F. Lewis, and P O’Byrne. The alcubierre warp drive: On the matter of matter.

[15] M. S. Morris, K. S. Thorne, and U. Yurtsever. Wormholes, time machines, and the weak energy condition. Phys. Rev. Lett., 61(13):1446–1449, 1988.

[16] A. Ori. Must time-machine construction violate the weak energy condition? Phys. Rev. Lett., 71:2517–2520, 1993.

[17] A. Ori. A class of time-machine solutions with a compact vacuum core. Phys. Rev. Lett., 95(021101), 2005.

[18] E. Poisson. A Relativist’s Toolkit: The Mathematics of Black- Hole Mechanics. Cambridge University Press, 2007.

[19] E. Poisson and W. Israel. Inner-horizon instability and mass inflation. Phys. Rev. Lett., 63(16):1663–1666, 1989.

[20] F. J. Tipler. Rotating cylinders and the possibility of global causality violation. Phys. Rev. D, 9(8):2203–2206, 1974.

[21] A. Tomimatsu and H. Sato. New series of exact solutions for gravitational fields of spinning masses. Prog. Theor. Phys., 50(1):95–110, 1973.

[22] W. J. van Stockum. The gravitational field of a distribution of particles rotating around an axis