"RADIOTEKHNIKA" , 2010, №2

UDC 625.371.526.

 

Influence of width of the line of optical radiation of the laser of a rating on a radio-frequency range of the optoelectronic  oscillator.

 

Bortsov Alexander A., Ilyin Yuri B.

 

MPEI (TU), NPO KVANT-DAYNA, This email address is being protected from spambots. You need JavaScript enabled to view it.

 

Theoretical and experimental studying of the low-noise optoelectronic  oscillator (OEO) with the dispersive fiber-optical line of a delay as systems of two oscillators of optical and radio-frequency ranges is carried out. One of oscillators - the laser serves as a rating for the second - the radio-frequency oscillator. It is shown that the OEO is the radio-frequency oscillator with the ultralow level of spectral density of phase noise (settlement size - 170db/Hz at a generation frequency 10 GHz when detuning 1 kHz).

 

 

 1. Introduction

 

The optoelectronic  oscillator   (OEO) with the fiber-optical line of a delay (FOLD) [1-6] is a perspective source of the 4...100 GHz. The optoelectronic  oscillator  OEO can be used as the setting oscillator in devices of radio - and optical locational complexes [7], and also in systems of formation and processing of optical and electronic precision signals, for example, with impulse duration about a picosecond [8]. The OEO  executed on the basis of optical microresonators [9] has small dimensions, weight and cost. Experimental results of measurements of spectral density of phase noise of such oscillator, equal-147 dB/Hz at a frequency of generation of 10 GHz at standard detuning of 1 kHz, allow to conclude that the OEO competes with low-noise microwave ovens generators with dielectric resonators on sapphire crystals at frequencies of generation of 8... 70 GHz [10]. Methods of phase stabilization of self-oscillations the OEO are developed [11,12]. Radio-frequency filters with on the basis of optical microresonators [13] which good quality on the microwave oven already makes more than 30000 are improved. Less than 100 cubic millimeters will be in the long term received super low-noise the OEO with overall dimensions.

 At the same time influence of width of the spectral line of optical radiation of the laser - basic element the OEO - on spectral characteristics of generation of radio-frequency fluctuations is a little studied.

      

    The purpose of work is establishment of dependence of spectral density of power of phase noise radio-frequency the OEO from width of the spectral line of optical radiation of the laser.

 We will analyse the OEO as system of two various generators - the optical quantum generator with a generation frequency approximately $\boldsymbol{\nu}_{0}$ =100...200 THz and the radio-frequency oscillator with a frequency of generation of $f { } _ {0} $ =4... 100 GHz. Thus the optical quantum generator is a rating source for the radio-frequency oscillator. In both generators their ranges are formed by the fluctuations having the different nature, and width of the spectral line of radio-frequency self-oscillations is defined by parameters of two self-oscillatory systems - the laser and the oscillator. The OEO is interesting feature that the range of radio-frequency fluctuations of generation is formed not only noise having the electronic nature but also the phase fluctuations of optical radiation of the laser which have the quantum nature and are defined by the spontaneous radiation of the laser. Consideration the OEO as sets of two self-oscillatory systems with dissipation gives the chance to analyse influence of characteristics of the laser on noise the OEO, to investigate further possibility of management of a signal the OEO by means of change of optical frequency and a range of the laser, to study synchronization the OEO an external optical source of radiation, etc.

 Lower for simplicity and identification of influence of noise of radiation of the laser on noise the OEO is considered that noise of the photodetector, noise of the electronic nonlinear amplifier are small and they can be neglected.

           

 2. Device and principle of work OEO

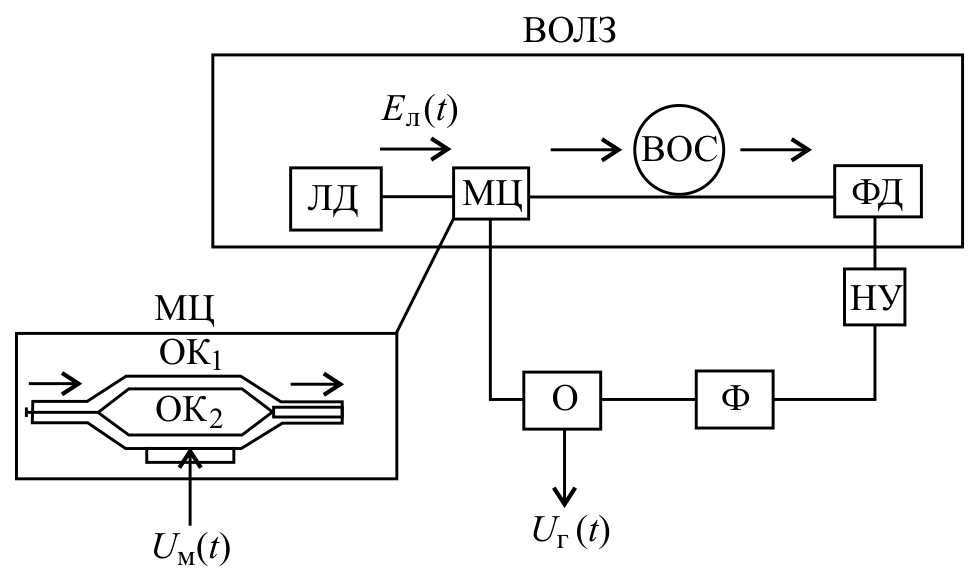
 The  optoelectronic oscillator  consists as it was told, from two self-oscillatory systems - the laser (or the laser diode (LD - ЛД)) and the radio-frequency oscillator (fig. 1). The laser is a rating for the oscillator which is formed, consistently closed in a feedback ring by the electro-optical modulator of the Makh- Zander (MZ - МЦ), the fiber-optical system (FOS -ВОС), the photo diode (FD -ФД), the nonlinear amplifier (NA- НУ), the radio-frequency narrow-band filter (А-Ф ) and an connector (О). The OEO mathematical model with the quantum-dimensional laser diode is in detail studied in [14,15].

              

                                                                  а)

 

                        

                                                                   б)

 

Fig. 1. Scheme (and) and photo experimental sample of the microwave oven low-noise laser oscillator of range. LD (LD-ЛД) - the laser diode, MTs (MZ- МЦ) – the electrooptical Makh-Zendera modulator, BOC (FO) - the fiber-optical light guide, FD(PD) - the photodetector, НУ - the nonlinear amplifier, F-A - the radio-frequency filter, O - the connector.

 

Optical radiation (bearing) of the laser arrives on an entrance of the MTs optical modulator in which radiation is modulated by an electric signal of      $u=u_{g} (t)$. Further optical radiation via the optical modulator, and fiber-optical system arrives on an entrance of the photodetector (FD). The radio-frequency fluctuations (subbearing) received at the photodetector exit take place through the nonlinear amplifier (NA), the frequency-selective filter (F - Ф) and go on this ring system through an connector to the microwave  the MZ modulator entrance.

 In system the LOG when performing conditions of self-excitation in electronic part of such oscillator there are radio-frequency fluctuations of $u=u_{g} (t)$. Thus on an electronic entrance of MZ from an exit of the nonlinear amplifier through an connector in the course of generation of self-oscillations the radio-frequency signal, which instant tension arrives

 

\begin{equation} \label{GrindEQ__1_} u_{g} (t)=U_{0} \cos (2\pi f_{0} t+\phi _{0e} ) {}, (1)     \end{equation}      

 

where $U_{0} =U_{0M} =U_{0F} $,  ${}_{ }$ - amplitude of self-oscillations on an entrance of the MTs modulator or an exit of the filter F, $ f_{0} $ - a radio frequency of self-oscillations, $\phi _{0e} $ - continuous phase shift.

 In a further statement we will consider the LOG in which the laser is a high-coherent source of optical radiation and line width $\Delta \nu _{L} \ll f_{0} $. The Makh-Zender modulator represents two strip optical wave guides connected on an entrance and an exit of Y - optical otvetvitel (fig. 1). When using in the OEO optoelectronic oscillator of the single fiber light guide (FLG), the difference in $T_{{\rm M20}} $ and $T_{{\rm M10}} $ in channels of the modulator makes 

 

\begin{equation} \label{GrindEQ__2_} {\rm \; }\Delta T_{{\rm M}} {\rm \; =\; }T_{{\rm M20}} {\rm -\; }T_{{\rm M10}}{}{},(2) \end{equation}           

 

  The fiber optical line of a delay in the OEO is generally dispersive, that is delay time  is function of optical frequency of the laser

 

\[T_{{\rm BC}} =T_{{\rm BC}} {\rm (}\nu _{} {\rm )}{},{} . (3)\]

 

Thus, the OEO optoelectronic generator represents the closed self-oscillatory system with dissipation which part the dispersive line of a delay is.

             

 2. Mathematical model optoelectronic oscillator  OEO

 For identification of the main mechanisms of formation of a radio-frequency range results of the analysis of systems of the differential equations with fluctuations for the laser and the optoelectronic oscillator  are given in system the OEO below.

 

2.1 The laser in the  optoelectronic  oscillator 

 We will give the fluctuation equations for it removed with use of the semi-classical theory [17, 18, 19] for reflection of the main spectral properties of the laser below. Dynamic character of noise characteristics of the laser can be described by means of the equations for intensity of electric field of $ E_{L} $ and an optical phase  $\varphi _{L} $  the laser

 

\begin{equation} \label{GrindEQ__4_} {\rm \; }dE_{L} {\rm /}dt{\rm \; =\; [}\alpha _{0L} -{\rm (2}\pi \nu _{0P} {\rm /}Q_{0L} )-\beta _{0n} E_{L} ^{2} ]E_{L} -\xi _{\beta AM},{}{}(4) \end{equation}                    

\begin{equation} \label{GrindEQ__5_} {\rm \; }[2\pi\nu _{0} - \Omega _{L} +d\varphi_{L} {\rm /}dt{\rm \; ]E_{L}=\; [}\sigma _{0L}E_{L} +\rho _{0L} E_{L} ^{3} ]-\xi _{\beta FM},{}{}(5) \end{equation}                    

 

 where $\alpha _{0L} $  - optical strengthening of the active environment of the laser,

$\nu _{0P}$   -- own frequency of the resonator of the laser,

$Q_{0L} $ -- quality of the resonator of the laser,

$\beta _{0n} $ -a factor of spontaneous radiation of the active environment,

$\Omega _{L}$ --the angular optical frequency of the longitudinal generated fashion of the resonator of laser $\Omega _{L} =2\pi c(n_{L} L_{0L} )^{-1}$ ,

$n_{L}$ - index of refraction of material laser,

$L_{0L}$ - the geometrical length of the resonator of the laser,

$c$- velocity of light in vacuum,

$\varepsilon _{{\rm 0}}$ - a dielectric constant ,

$\sigma _{{\rm 0}}$, $\rho _{0L}$ -constant coefficients,

$\xi _{\beta AM} $, $\xi _{\beta FM}$ --inphase and quadrature components "lanzhevenovsky" of phase fluctuations .

 

Their spectral density are equal according to $S_{\beta AM}$  to $ and $S_{\beta FM}$ which are defined by noise of a field of atoms of the active environment in the laser resonator.

Taking into account generation of the laser in a limited strip of optical frequencies casual process of optical radiation of the laser can be considered stationary with zero average value. For such process spectral density of $S_{mL} {\rm (}\nu {\rm )}$ and $S_{\psi L} {\rm (}\nu {\rm )}$ fluctuations of the laser of  $m_{L} (t)$ , $\psi _{m} (t)$ are at the solution of the truncated equations (4) and (5) taking into account fluctuation "lanzhevenovsky"of influences of $S_{\beta AM}$,  $S_{\beta FM}$ and make a laser range. The spectral line of radiation of the laser can be described approximately Lorentz's function in which width the strip of radiation of the laser is equal $\Delta \nu$.

 From a laser exit linearly polarized optical radiation of $E_{L}^{} $ arrives on the MZ modulator entrance. Thus dependence on time of $t$ instant intensity of a field of radiation of $E_{L}^{} $ at the central frequency $\nu _{0} $ generation of the laser taking into account amplitude and phase fluctuations of the laser  is defined by expression

\[{\rm \; }E_{L} {\rm \; =\; (}E_{0L} {\rm +}m_{L} )\exp [j(2\pi \nu _{0} t-\varphi _{0L} -\psi _{m} )]                                                        {}{}, (8)\]

where ${\rm \; }m_{L} {\rm \; =\; }m_{L} {\rm (}t,R)$,  ${\rm \; }\psi _{m} {\rm \; =}\psi _{m} {\rm (}t,R)$ - amplitude and phase fluctuations of a field of $E_{L}^{} $ the laser determined by spectral density of expressions (6) and (7), respectively, $R$ - the index considering spatial dependence of optical radiation of the laser, ${\rm \; }E_{0L} {\rm \; =\; }E_{0L} {\rm (}R)$ - the partsialny amplitude of radiation of the laser of ${\rm \; }\varphi _{0L} {\rm \; =}\varphi _{0L} {\rm (}R)$ - partsialny phase attack of intensity of radiation of the laser.

          

 Fig. 2. The spectral density of power of optical radiation of the laser of a rating in the OEO depending on detuning V at various values differences of optical frequencies. V=$\Delta \nu _{}$=$\nu _{} - \nu _{0}$, and $\nu _{}$ and $\nu _{0}$ - the current and central optical frequency of radiation of the laser. Computer modeling was made at

$ \frac{\Delta \nu _{} }{\nu _{0}}=10^{-6}$,

$\Delta \nu _{}$ = 129 MHz,

$\nu _{0}$ =$129 · 10^{12} $Hz

$ \frac{\Delta \nu _{} }{\nu _{0}}$=  $10^{-10}$ (a curve 1), $10^{-8} $(a curve 2); $10^{-7}$  (curve 3).

 

     

2.2 The modulator in the OEO

Optical radiation of the laser passes the MZ modulator, the  fiber light guide and arrives on a reception platform of the FD photo diode. On a platform of the FD photo diode there are two optical radiations which passed the MZ modulator for the first $ {\rm \; }E_{1L} {\rm \; =\; }E_{1L}(R)$ and second $ {\rm \; }E_{2L} {\rm \; =\; }E_{2L}(R)$ to optical channels

                                        

 \begin{equation} \label{GrindEQ__9_} {\rm \;} E_{1L} {\rm =\; }k_{01} \cdot {\rm (}E_{0L} {\rm +}m_{L} )\exp [j2\pi \nu _{0} (t+T_{M1} +T_{{\rm BC}} )-j\varphi _{0L} -j\psi _{m1}] (9)\end{equation}

\begin{equation} \label{GrindEQ__10_} {\rm \;} E_{2L} {\rm =\; }k_{02} \cdot {\rm (}E_{0L} {\rm +}m_{L} )\exp [j2\pi \nu _{0} (t+T_{M2} +T_{{\rm BC}} )-j\varphi _{0L} -j\psi _{m2}] (10)\end{equation}  

 

With a small amplitude of tension of an entrance signal of modulation on MTs it is possible to use linearization of argument of ${\rm arg}_{12L} $  and for convenience in the coefficient of transfer of the MTs modulator of  

\[M_{z} {\rm =}k_{01} \cdot \{ 1-\cos {\rm \; }[2\pi \nu _{0} (T_{M20} -T_{M10} )]\}^{1/2}\].

 

             

2.3 The spectral density of $S{}_{\boldsymbol{\mu} }( \boldsymbol{\omega})$ the photodetected fluctuations of the laser

As a result of photodetection at the FD photo diode exit in the course of establishment of self-oscillations in the closed system the OEO is formed a harmonious radio-frequency signal at a frequency $f_{0} $ with noise. The radio-frequency noise in the OEO caused by noise of the laser can be interpreted as transformation of fluctuations. It is possible to consider that in optical part the LOG is formed by the MTs modulator and the light guide the interferometer with different geometrical lengths of shoulders. The interferometer together with the photo diode will transform frequency (or phase) noise of the laser to phase noise of photocurrent. Noise at FD exit in the opened system the OEO is defined by the conversion noise of the laser of pro-detected by AM-FM $S_{\mu AM-FM} $, FM noise of the laser of $S_{F} {\rm (}\omega {\rm )}$ and AM noise of $S_{\mu AM} $ the laser. AM, as a rule, can be neglected noise because of their trifle. As a result of the carried-out analysis the spectral density of fluctuation of currents determined by noise of the laser at the photo diode exit the LOG is equal in the opened system

\[{ \ \; }    S_{\mu}(\omega)= S_{\mu AM} {\rm \; }+S_{\mu AM-FM} +S_{F} \]     

                     

\begin{equation} \label{GrindEQ__12_} {\rm \; \; }S_{\mu AM} {\rm (}\omega _{} {\rm )=\; }\frac{S_{\beta AM} D_{AM} \cdot U_{0M}^{2} }{(\omega _{} -\omega _{0} )^{2} T_{0L}^{2} \cdot 0,25+B_{L}^{2} } {},{} (11)                       {\rm \; \; }S_{\mu AM-FM} {\rm =\; \; }\frac{4\cdot S_{\beta _{} } D_{FA} \cdot U_{0}^{2} \cdot \sin [2\pi \nu _{0} (T_{M1} -T_{M2} )]\cdot G_{12} }{(\omega _{} -\omega _{0} )^{2} T_{0L}^{2} \cdot B_{L}^{2} }{},  (12)\end{equation}

 

\begin{equation} \label{GrindEQ__13_} S_{F} {\rm (}\omega {\rm )\; }\approx \frac{4\cdot S_{\beta _{} } D_{FM} U_{0}^{2} \cdot G_{12} }{(\omega -\omega _{0} )^{2} T_{0L}^{2} \cdot B_{L}^{2} },{}{} (13)\end{equation}

 

 where $G_ {12}$ - coefficient of suppression of phase fluctuations of optical radiation of the laser which is defined as $G_{12} =1-[(\gamma _{1L\psi } -\gamma _{2L\psi } )+\exp (-\Delta T_{M} \cdot \Delta \nu _{L} )]^{} $, $\gamma _{1L\psi } $ and $\gamma _{2L\psi } $ - spatial constants of fluctuations of a phase of radiation of the laser at the exit of OK1 and OK2 channels of the Makha-Zendera modulator respectively. In practice to create ideal, identical optical channels in MTs directed the otvetvitelyakh it isn't possible and really coefficient of suppression of составляет $G_{12} \approx 10^{-1} -10^{-3} $ . The main mechanisms of formation of noise at the photo diode exit in the opened system the OEO with the Makha-Zender modulator are: transformation or conversion of phase noise of the laser in amplitude, suppression of conversion and phase noise with coefficient of $G_{12} $ due to coherent addition of fluctuations with different, but approximate equal delays at the photo diode exit.

     

 

2.4 The differential equations of the OEO optoelectronic generator with fluctuations

 

The differential equation for the OEO taking into account the pro-detected fluctuations of the optical bearing is removed in the assumption that nonlinearity of the  amplifier is defined by the average steepness of $S_{{\rm HY}} $, and filter parameters - own frequency of $f_ {F0} of $ and a constant of time of $T_{F} $ respectively. Thus amplitude of self-oscillations of $u(t)$ the LOG is defined as

 

\begin{equation} \label{GrindEQ__14_} {\rm \; }\frac{d^{2} u}{dt^{2} } {\rm +}\frac{1}{T_{F} } \cdot \frac{d^{} u}{dt} {\rm +\; 2}\pi f_{F0} u{\rm =\; }S_{{\rm HY}} [E_{0L}^{2} K_{BLZ} \cdot u(t-T_{BC} )]+\Psi _{n}{}  {}, {} (14) \end{equation}

 

   where $\Psi _{n} $ - the noise component of tension at the photo diode exit formed by the pro-detected fluctuations of a phase and amplitude of the optical U-0024 bearing the laser, and $\Psi _{n} =S_{{\rm HY}} \cdot K_{BLZ} \cdot \mu _{n} $. The differential fluctuation equation together with (4-5) for the laser forms full system of the equations with fluctuations. They allow to find solutions for radio-frequency ranges at different sizes of width of the line of laser $\Delta \nu _{} $ which are presented in fig. 3 - 6.

 

                  

                         2.5 Range of radio-frequency fluctuations of the OEO 

Using expressions (11) - (13) and the equations (14) approximate expression for the spectral density of power of phase noise OEO ${\rm \; }S_{\Psi AG} $ from frequency detuning $\omega -\omega _{0} $:

 

    \begin{equation} \label{GrindEQ__15_} S_{\Psi AG} {\rm (}\omega _{} {\rm )=\; }\frac{4(\Delta \nu )^{2}S_{\beta }k_{E}D_{FM}G_{12} (1+\sin (\nu _{0} \cdot \Delta T_{M} )}{ (\omega _{} -\omega _{0} )^{2}T_{0L}^{2} \cdot \left|K_{BLZ} \right|\cdot E_{0L}^{2} \cdot [1+\cos (\omega -\omega _{0} )T_{BC} ]^{2}   }.{}{}{} (15)\end{equation}

 

 Expression (15) establishes connection of ${\rm \; }S_{\Psi AG} $ with a width of the spectral line of radiation of laser $\Delta \nu $, a difference of delays in modulator MZ  $\Delta T_{{\rm M}} $, a delay of VS of $T_{BC}^{} $ and capacities of the laser. Influence of width of the line of laser $\Delta \nu $ for spector $S_{\Psi AG} (\omega )$ especially is shown when detuning from carrier frequency $\omega -\omega _{0} \approx 2\pi \cdot \Delta \nu _{} $comparable with $\Delta \nu _{} $. At big detuning $\omega -\omega _{0} \gg 2\pi \cdot \Delta \nu _{} $ spector $S_{\Psi AG} (\omega )$  is defined by time of delay of $T_{BC} $  in the light guide.

  At a big difference of delays in channels of the modulator, for example, at $\Delta T_{{\rm M}} =10^{-4} c$, at $T_{BC}^{} =10^{-9} c$, $\Delta \nu _{} \approx 10^{3}$Hz from (15) follows,  that

   

 \begin{equation} \label{GrindEQ__16_} {\rm \; }\Delta f_{0,5} \approx 3,8\cdot \Delta \nu _{} ^{3/4}{}{}.(16) \end{equation}                                            

                                          

In this case at $(\Delta T_{M} \cdot \Delta \nu _{} )\to 1$  with the help the OEO can perform measurements of width of the spectral line of laser

 

\[\Delta \nu _{} ^{} {\rm \; }\approx [\Delta f_{0,5}^{4/3} ]/3,8^{4/3} \].

 

On the contrary, at a small difference of delays in channels of the modulator that is when work of $(\Delta T_{M} \cdot \Delta \nu )\to 0$, the LOG is the low-noise oscillator with extremely low level of phase noise. For example, at a small difference of delays in channels of modulator $\Delta T_{{\rm M}} =10^{-12} с $, ${}$ $\Delta \nu \approx 10^{3} $Hz, ${}$ $T_{BC}^{} =10\cdot 10^{-6} $ с, ${}$ $G_{R} =0,999$, ${}$ $S_{\beta _{} } \cdot D_{FM} =10^{-12} $ width of the OEO spectral line is about four orders less than width of the line of the laser

 

\begin{equation} \label{GrindEQ__17_} {\rm \; }\Delta f_{0,.5} \approx 3,8\cdot 10^{-4} \cdot \Delta \nu _{} ^{3/4} {}(17).  \end{equation}  

               

                                

3. Results of computer modeling OEO

 The solution of the equation (14) allowed to find ranges of tension of self-oscillations of $u_ {g} (t)$ of  the OEO by means of numerical methods, using applied programs of a MATLAB package, for different values of width of the spectral line of the laser (fig. 3) and different sizes of delays of $T_ {BC} ^ { } $. In fig. 3 the spectral density of power of phase fluctuations of the laser taken at numerical modeling with laser radiation strip width $\Delta \nu _{} $= 10kHz ( curve 1) are presented,  1 MHz ( curve 2); and 10 MHz ( curve 3) at $\nu_{0} =1,29\cdot 10^{14} $${}^{ }$Hz. Thus spector were approximately described by Lorentz's function.

                                                                                       

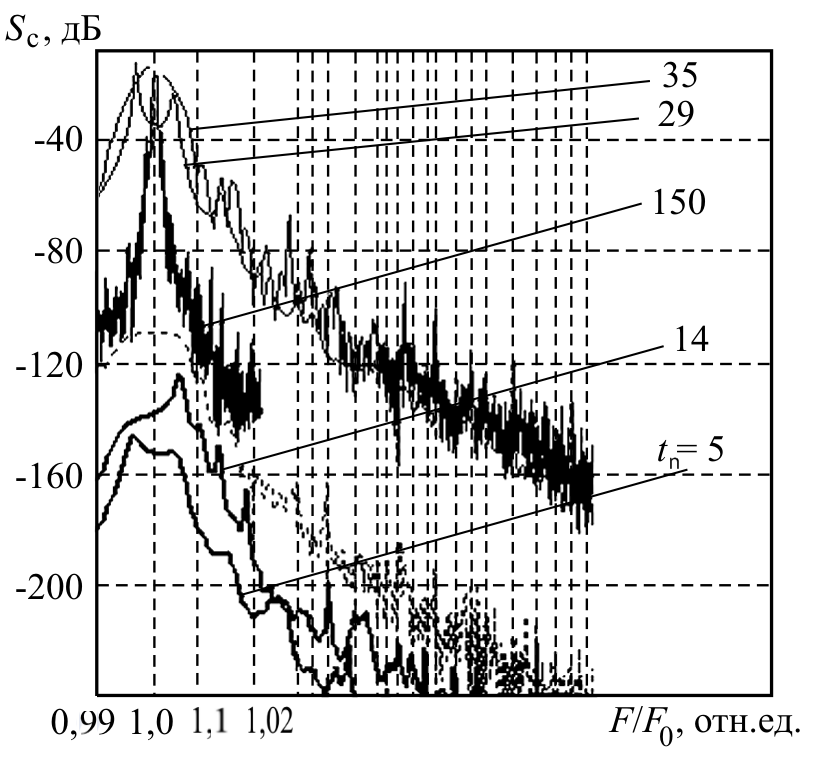
Fig. 3. The spectral density of power of phase noise of radio-frequency self-oscillations the OEO from relative detuning for different sizes of rated time of supervision of transition process of the subbearing

$t _{0}$ =$5, 14, 29, 35, 150$.

 $t_{0} $ is rated time of the beginning   of development of  of radio-frequency oscillations $t _{1}$ in the  optoelectronic oscillator OEO. Rated time from a reference mark for the period of a delay in VOLZ 

$t _{0} = \frac{t _{1}}{ T_{BZ} }$.

Computer modeling was made at values

$ \frac{\Delta \nu _{} }{\nu _{0}}=10^{-6}$,

$\Delta \nu _{}$ = 129 MHz,

$\nu _{0}$ =$129 · 10^{12} $Hz.

 

 

The question of formation of a range subbearing the LOG was studied and solutions of a range subbearing for various times of transition process (fig. 3) (for laser spector width $\Delta \nu _{} $=129 MHz, $\frac{\Delta \nu _{} }{\nu _{0}} $=$10^{-6}$, by $\Delta \nu _{} =1,29 \cdot 10^{14}$ Hz). In fig. 3 it is visible that process of formation and establishment of a range the LOG takes long time to multiple about 100 times of a delay in the light guide.

 

In fig. 4 and fig. 5 results of numerical modeling of spectral density of phase noise for the OEO with not dispersive and dispersive line of a delay are shown. As a result of research conclusions are drawn that at small delays in the light guide the OEO with not dispersive line of a delay has considerable impact on a range the noise connected with phase and amplitude conversion (fig. 4). At increase in width of the line of the lazera $\Delta \nu _{} $ Delta in a spector of the OEO appear additional noise components.

        

Fig. 4. The spectral density of power of phase noise of radio-frequency self-oscillations the OEO from not dispersive VOLZ from detuning on a radio frequency from width of spectral density of optical radiation of the laser subbearing 8,2 GHz at different values. Computer modeling on the basis of the fluctuation equations (18) OEO at $\Delta \nu _{} $ = 10kHz (a curve 1), 1 MHz (a curve 2); and 10 MHz (a curve 3) at $\nu _{0}$ =129 · 1012 Hz. The dispersive steepness of delay in the light guide made 10-7, length of the light guide-200 m. Dependences at $\Delta \nu _{} $ = 50 MHz (a curve 4) и при  $\Delta \nu _{} $ =10 кГц (кривая 5) .    

 

 

                                             

Fig. 5. The Spectral density of power of phase noise from relative detuning (radio-frequency subbearing) self-oscillations the LOG with the dispersive fiber-optical line of a delay. The dispersive steepness of delay in the light guide, length of the light guide is $L=1000$ m. Computer modeling on the basis of the fluctuation equations (18) OEO ${}{}$at $\Delta \nu _{}$= 10 kHz ( curve 1), 1 MHz ( curve 2); and 100 MHz (curve 3). 

  

In the optoelectronic oscillator OEO with the dispersive line of a delay the increase in width of a range of the laser (fig. 5) more than 100 MHz is led due to dispersion of the fiber light guide to considerable expansion of a range by the LOG. Due to dispersion of the light guide the range has remarkable feature - edge structure - periodic dependence on detuning on a radio frequency. The period of this dependence is proportional to work of time of dispersion in the light guide on   laser radiation strip width $DF\sim \Delta v\cdot \tau _{D} $  . When using highly dispersive light guides or low coherent lasers with a width of line more than 100 MHz in the spectral line of generation the LOG ostsillyation on detuning frequency are observed. Such edge structure of a radio-frequency range the LOG is similar to structure of optical spectra of laser diodes with highly dispersive active environments.

                                   

 4. Experimental researches

 Some prototypes the the optoelectronic oscillator OEO of range of the microwave oven with different laser diodes of a rating radiating on lengths of waves 1310 nanometers or 1550nm with the maximum output power of optical radiation approximately from 10 to 20 mW were experimentally investigated. In fig. 1 (b) the photo of one of samples collected according to the scheme of fig. 1 (a) is presented . As the photodetector the FD photo diode on the basis of InGaAs was used. The radio-frequency filter represented the microwave  dielectric resonator with the loaded good quality of $Q\approx 1000$ executed on ceramics and with an own frequency about 8,2 GHz. In the model it had took place broadband to $ 15$ GHz, modulation of laser radiation which was carried out by the Makh-Zender modulator of Hitachi firm. When carrying out experiments single-mode light guides with lengths from 60 m to 4640 m were used. Experimental amplitude and frequency adjusting curves are given in fig. 6. With different lengths in system the OEO it is received steady generation single-frequency self-oscillations at a frequency close to 8,2 GHz. In fig. 6 in in experimental frequency dependences on current of a rating of the laser diode it is possible to observe jumps of frequency (fig. 6 b) that is connected with reorganization of frequency on the next types of oscillations. In the OEO it is received short-term (on an interval of time of 1 min.) relative instability of frequency (mean square according to Allan) the generated $1\cdot 10^{-8} $ subbearing not worse at the room temperature. Level of phase noise when using various lasers of a rating made $S_ {c} \approx$ - 80 ...-140 dB/Hz on detuning of 1...10 kHz from the frequency generated by the microwave oven subbearing (fig. 4) and depended on width of the line of radiation of the laser. These experimental dependences will well be coordinated with settlement at the accounting of stabilization effect on lengths of the fiber light guide more than 50 m. Not compliance of settlement and experimental curve phase noise of $S_ {c} $ is explained by influence on them of polarization and heterogeneity on space of radiation of real laser sources which weren't considered at calculation.

                      

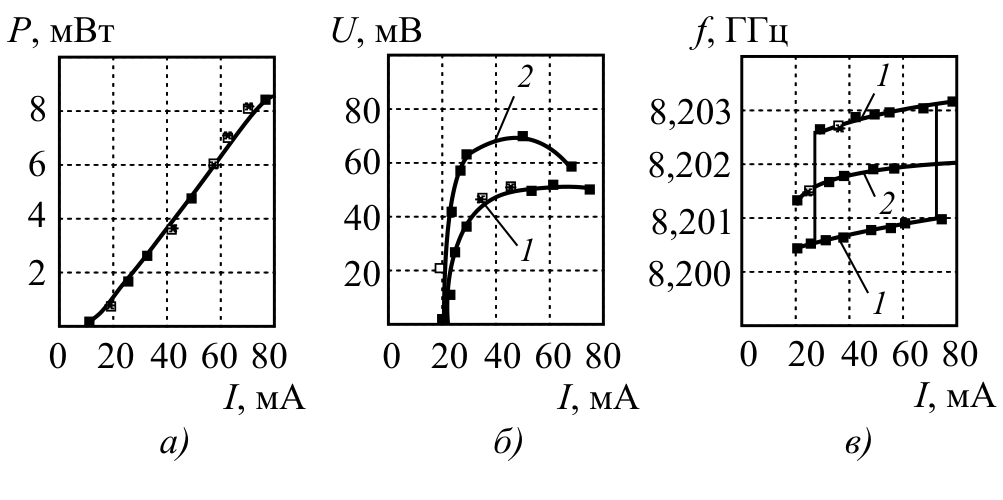
Fig. 6. Experimental dependences in the OEO of the microwave oven of range on current of shift and) capacities of the laser diode, b) amplitudes of tension of self-oscillations at an average radio frequency of self-oscillations of =8,2 GHz, c) radio frequencies of self-oscillations for various lengths of light guides 60m (1) and 70 m (2).

                                 

 

5. Conclusions.

 The carried-out analysis showed that a spector of the OEO optoelectronic oscillator the pro-detected conversion phase and amplitude noise and phase fluctuations define noise of optical radiation of the laser. The size of spectral density of power the OEO is proportional to a square of width of the line of optical radiation of the laser. The increase in width of the spectral line of the laser of a rating leads the OEO to expansion of a radio-frequency range. On condition of respectively small and big difference of delays in channels of the OEO with MZ modulator it is possible to use respectively as the low-noise oscillator with record-breaking small levels of phase noise or \textit { the measuring instrument of small width of the spectral line of radiation of lasers less 10 kHz.

 

6. Anknowlegements.

 Authors express gratitude for the shown interest and participation in discussions to professor Udalov N. N. and professor Kapranov M. V.

 

7. Literature:

 

1.Nakazawa M., Nakashima T., Tokuda M. An optoelectronic self-oscillatory circuit with an optical fiber delayed feedback and its injection locking technique.//J/Lightwave Technol. - 1984. - V.2, No. 5, - P. 719-730.

 

2. Grigoryants V. V., Dvornikov A.A., Ilyin Yu.B. and Konstantinov V. N. Prokofiev V. A. Generation of radio signals in system ''the laser - the optical line of a delay''.//Quantum. electron. - 1984. - T.11, No. 4. - Page 766-775.

 

3. Grigor'yants V.V., Il'in YU.B. Laser optical fiber heterodyne interferometer with frequency indicating of the phase shift of a light signal in an optical waveguide.//Optical and quantum electronics.-1989.-№ 21. - P.423-427.

 

4. Bortsov A. A., Grigoryants V. V., Ilyin Yu. B. Influence of efficiency of excitement of light guides on oscillator frequency with the differential fiber-optical line of a delay//Radio engineering. - 1989 - No. 7. - S.84-89.

 

5. А.с.№1538265 USSR, MKI3 H03K 9/00A. Device of functional transformation to A. A. frequencies / Fighters, Ilyin Yu. B., etc. (USSR). - 9 with.-1989 g.

 

6. X. S. Yao and L. Maleki, ''Optoelectronic microwave oscillator,'' \textit { J. Opt.Soc. Amer. B, Opt. Phys. }, vol. 13, no. 8, pp. 1725 - 1735, 1996.

 

7. Bortsov A. A., Ilyin Yu. B. The microwave oven differential optoelectronic oscillator with the lowest level of phase noise//Radio optical technologies in instrument making: Tez.dokl. The II-nd научн. - техн. конф. 14 - On September 21, 2004 - Sochi, 2004 - S.84-86.

 

8. J. J. McFerran, E. N. Ivanov, A. Bartels, G. Wilpers, C. W. Oates, S. A. Diddams, and Hollberg, ''Low-noise synthesis of microwave signals from an optical source,'' Electron. Lett. 41, 650-651 (2005).

 

9. Savchenkov, A. A. Ilchenko et al.  Low Threshold optical oscillations in a whispering gallery mode CaF2 resonator. Physical Review Letters 93, 243905 (2004).

 

10. Tsarapkin D.P - Methods of generation of the microwave oven of fluctuations with a minimum level of phase noise: The thesis on competition of the Doctor of Engineering. - M, 2004. - 413 pages.

 

11. Patent for the invention No. 2282302 RU, MPK 3 7 H03 C3/00. The shaper of a frequency-modulated signal / A. A. Fighters, Ilyin Yu. B. - 10 pages of 2004.

 

12. Patent  No. 44902 RU, МПК$ { } ^ {3} $7 H03 C3/00. The shaper of a frequency-modulated signal / A. A. Fighters, Ilyin Yu. B. - 10 pages of 2004.

 

13.  A. A. Savchenkov, A. B. Matsko, V. S. Ilchenko, and L.Maleki, ''Optical resonators with ten million finesse,'' Opt. Express \15, 6768-6773 (2007).

 

14. A. A. Bortsov. Management of frequency in the laser oscillator with the compound fiber-optical line of a delay//Avtoref. edging. yew. on соиск. уч. step. Cand.Tech.Sci. - M.:MEI. - 2005. - Page.

 

15. Bortsov A. A. Fazochastotnaya and amplitude-frequency characteristics of the mezapoloskovy quantum-dimensional laser diode with a strip of frequencies of modulation to 12 GHz//Radio engineering - 2006 g2006 - Page 43 - 47

 

16. Lex M. Fluctuations and coherent phenomena. M.:Мир, 1974

 

17. Lebedev A.K. Theory of the laser M.: MEI, 1998

 

18. Zhalud V., Kuleshov V. of N. Noise in semiconductor devices. Under the general edition of A. K. Naryshkin. - M.: Sovetstky radio, 1977 of-416 pages.

  

 

Article came to editorial office of the Radiotekhnika magazine in July 8, 2008.

RADIOTEKHNIKA magazine, 2010,№2

{gallery}publication/Radote2010{/gallery}