Оптоэлектронный генератор СВЧ  с ПАМ. Устойчивость колебательного процесса в ОАГ (ОЭГ).

При  исследовании оптоэлектронного генератора с прямой амплитудной модуляцией или ОЭГ

ПАМ возникает вопрос о его устойчивости колебательного процесса. 

Существует две особые точки стационарного режима: начальное состояние (или точка 1) и

собственно рабочее стационарное состояние генератора (точка 2), в котором происходит колебательный

процесс .

 Ниже для уравнения ОЭГ ПАМ с лазерным диодом исследованы вопросы устойчивости этих двух

точек. Уравнение для ОЭГ ПАМ выведено в главе 5 докторской работы Борцова А.А..

Оно представляет собой ДУ четвертого порядка с запаздывающим аргументом с общей нелинейной

характеристикой    

 

                                                

 Последнему дифференциальному уравнению 4-го порядка  соответствует следующее   характеристическое уравнение

                                      

 При этом коэффициенты 

                                                        

 

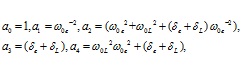
Понятие устойчивости системы оптоэлектронного генератора  связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

Понятие устойчивости можно распространить и на случай движения динамического процесса изменения переменной составляющей  напряжения на выходе (или переменной составляющей квадрата амплитуды напряженноси)  оптоэлектронного генератора :

• невозмущенное движение,
• возмущенное движение.

Оптоэлектронный генератор

Определение для ОАГ устойчивости по Ляпунову

 

Для ОАГ невозмущенное движение (при Δx_i∞=0) называется устойчивым по отношению к переменным x_i, если при всяком заданном положительном числе A2, как бы мало оно ни было, можно выбрать другое положительное число λ2(A2) так, что для всех возмущений Δxi0, удовлетворяющих условию:

i=0_n∑(μ_i2(Δx_i0)2)≤λ2,

возмущенное движение будет для времени t≥T удовлетворять неравенству:

i=0_n∑(μ_i2(Δxi)2)≤A2,

где: μi – коэффициенты, уравновешивающие размерности величин Δxi0.

Если с течением времени limΔxi→0, то система асимптотически устойчива.

Понятие о характеристическом уравнении

Было сказано, что устойчивость системы связана с природой самой системы, а не с тем, как внешние источники движущих сил (задание, помехи) заставляют перемещаться ее координаты. Очевидно, что невозможно описать цепь преобразования энергии (систему) не учитывая источников. Поэтому в правой части ДУ описывающих систему всегда будут присутствовать источники движущих сил (вспомните как записываются уравнения по II закону Кирхгофа). Однако если их обнулить, то система ДУ не потеряет смысла. После отключения источников в любой линейной цепи преобразования энергии возникнет переходный процесс обусловленный энергией, которую накопили пассивные реактивные элементы цепи (собственный переходный процесс). Именно он определит, будет ли система устойчивой. И именно эта система ДУ, в которой обнулены величины источников движущих сил, называется характеристической. Если система характеристических ДУ решена относительно одной из координат, то она называется характеристическим уравнением.

 

Оптоэлектронный генератор ПАМ. Условие устойчивости. Типы границы устойчивости

 

 

 

 

 

 

 

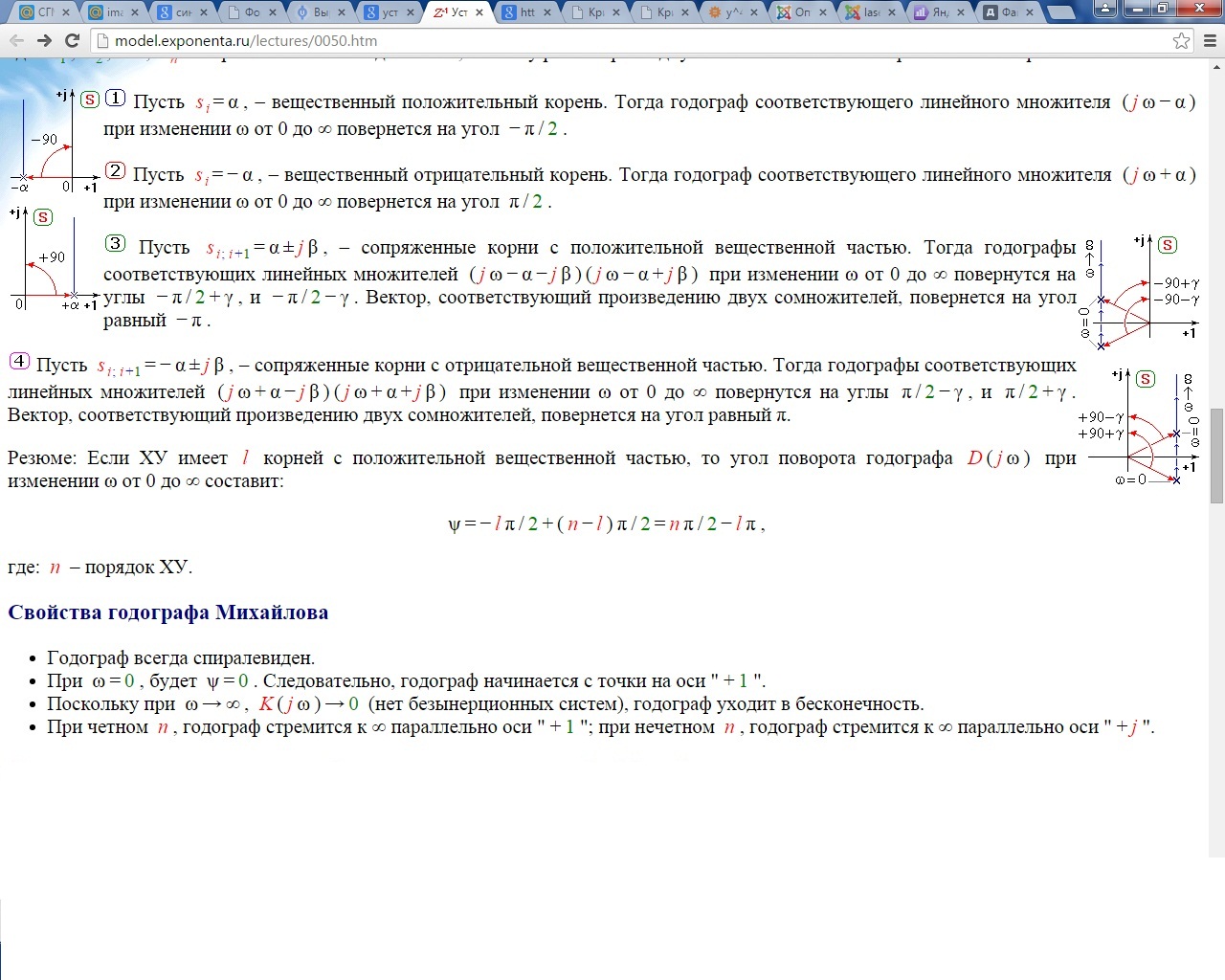
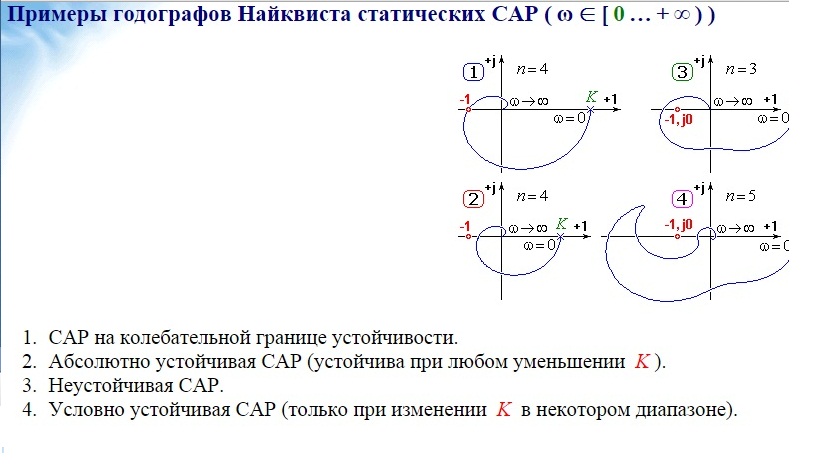
{jcomments on}

-