Влияние ширины линии оптического излучения лазера накачки на радиочастотный спектр лазерного автогенератора (оптоэлектронного генератора).
Журнал "РАДИОТЕХНИКА", 2010 г.,№2
УДК 625.371.526.
Влияние ширины линии оптического излучения лазера накачки на радиочастотный спектр оптоэлектронного генератора - лазерного автогенератора.
Борцов А.А., Ильин Ю.Б.
МЭИ(ТУ), НПО «КВАНТ-ДАЙНА», This email address is being protected from spambots. You need JavaScript enabled to view it.
Проведено теоретическое и экспериментальное изучение малошумящего лазерного автогенератора (ЛАГ) с дисперсионной волоконно-оптической линией задержки как системы двух автогенераторов оптического и радиочастотного диапазонов. Один из автогенераторов - лазер служит накачкой для второго -- радиочастотного автогенератора. Показано, что ЛАГ является радиочастотным автогенератором с сверхнизким уровнем спектральной плотности фазового шума( расчетная величина--170Дб/Гц на частоте генерации 10ГГц при отстройке 1 кГц).
Ключевые слова : оптоэлектронный генератор, лазерный автогенератор, волоконный световод, оптоэлектронный автогенератор .
1. Введение
Оптоэлектронный генератор или лазерный автогенератор (ЛАГ) с волоконно-оптической линией задержки (ВОЛЗ) [1-6] является перспективным источником СВЧ и КВЧ колебаний. ЛАГ может использоваться в качестве задающего генератора в устройствах радио- и оптических локационных комплексах[7], а также в системах формирования и обработки оптических и электронных прецизионных сигналов, например, с длительностью импульса порядка пикосекунды [8]. ЛАГ (или оптоэлектронный автогенератор), выполненный на базе оптических микрорезонаторов [9] имеет малые габариты, вес и стоимость. Экспериментальные результаты измерений спектральной плотности фазовых шумов такого автогенератора, равные -147 дБ/Гц на частоте генерации 10 ГГц при стандартной отстройке 1 кГц, позволяют заключить, что ЛАГ конкурирует с малошумящими СВЧ генераторами с диэлектрическими резонаторами на кристаллах сапфира на частотах генерации 8 ... 70 ГГц [10]. Разрабатываются методы фазовой стабилизации автоколебаний ЛАГ [11,12] . Совершенствуются радиочастотные фильтры с на основе оптических микрорезонаторов [13], добротность которых по СВЧ уже составляет больше 30000. В перспективе будут получены супер малошумящие ЛАГ с габаритными размерами менее 100 кубических миллиметров.
Вместе с тем влияние ширины спектральной линии оптического излучения лазера - базового элемента ЛАГ - на спектральные характеристики генерации радиочастотных колебаний мало изучено.
Целью работы является установление зависимости спектральной плотности мощности фазового шума радиочастотного ЛАГ от ширины спектральной линии оптического излучения лазера.
Проанализируем ЛАГ как систему двух различных генераторов -- оптического квантового генератора с частотой генерации примерно $\boldsymbol{\nu}_{0}$=200 ТГц и радиочастотного автогенератора с частотой генерации $f {}_{0 }$=4...100ГГц. При этом оптический квантовый генератор является источником накачки для радиочастотного автогенератора. В обоих генераторах их спектры формируются флуктуациями, имеющими разную природу, а ширина спектральной линии радиочастотных автоколебаний определяется параметрами двух автоколебательных систем -- лазера и автогенератора. Интересной особенностью ЛАГ является то, что спектр радиочастотных колебаний генерации формируется не только шумами имеющими электронную природу, но и фазовыми флуктуациями оптического излучения лазера, которые имеют квантовую природу и определяются спонтанным излучением лазера. Рассмотрение ЛАГ как совокупности двух автоколебательных систем с диссипацией дает возможность проанализировать влияние характеристик лазера на шумы ЛАГ, исследовать в дальнейшем возможность управления сигналом ЛАГ посредством изменения оптической частоты и спектра лазера, изучить синхронизацию ЛАГ внешним оптическим источником излучения и т.п.
Ниже для простоты и выявления влияния шумов излучения лазера на шумы ЛАГ считается, что шумы фотодетектора, шумы электронного нелинейного усилителя являются малыми и ими можно пренебречь.
2. Устройство и принцип работы ЛАГ
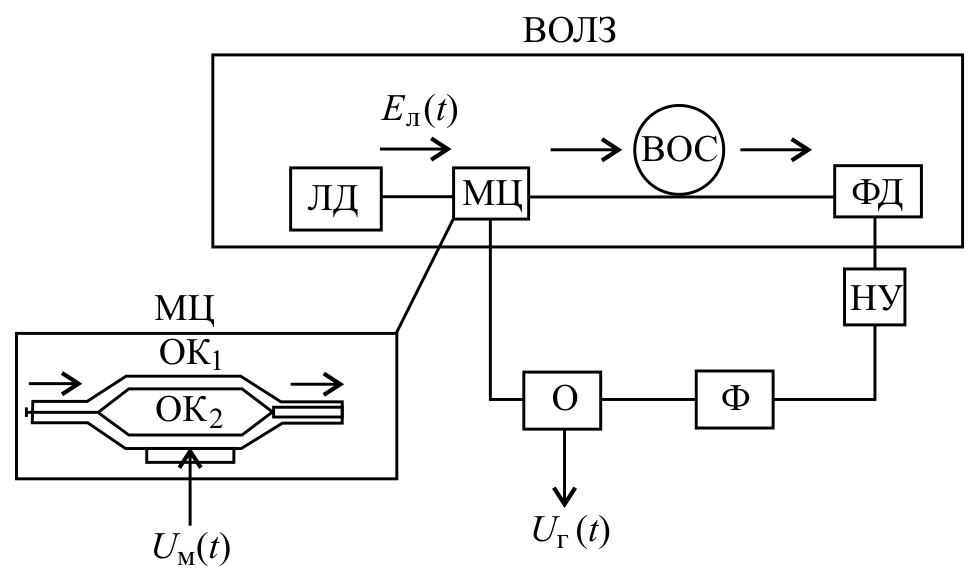
Оптоэлектронный генератор ЛАГ состоит, как было сказано, из двух автоколебательных систем -- лазера (или лазерного диода (ЛД)) и радиочастотного автогенератора (рис.1). Лазер является накачкой для автогенератора, который образован, последовательно замкнутыми в кольцо обратной связи электро-оптическим модулятором Маха-Цандера (МЦ), волоконно-оптической системой (ВОС), фотодиодом (ФД), нелинейным усилителем(НУ), радиочастотным узкополосным фильтром (Ф) и ответвителем(О). Математическая модель ЛАГ с квантоворазмерным лазерным диодом подробно изучена в [14,15].
а)

б)
Рис.1. Схема (а) и фото (б) экспериментального образца малошумящего лазерного автогенератора СВЧ диапазона.
ЛД (LD)-лазерный диод, МЦ (MZ) –электрооптический модулятор Маха-Цендера , ВОС (FO)- волоконно-оптический световод, ФД(PD)-фотодетектор, НУ- нелинейный усилитель, Ф- радиочастотный фильтр, О- ответвитель.
Оптическое излучение (несущая) лазера поступает на вход оптического модулятора МЦ, в котором излучение модулируется электрическим сигналом $u=u_{3} (t)$. }}Далее оптическое излучение через оптический модулятор, и волоконно-оптическую систему поступает на вход фотодетектора (ФД). Полученные на выходе фотодетектора радиочастотные колебания (поднесущая) проходят через нелинейный усилитель (НУ), частотно-избирательный фильтр (Ф) и направляются по этой кольцевой системе через ответвитель (О) на СВЧ вход модулятора МЦ.
В системе ЛАГ при выполнении условий самовозбуждения в электронной части такого автогенератора возникают радиочастотные колебания $u=u_{g} (t)$. При этом на электронный вход МЦ с выхода нелинейного усилителя через ответвитель О в процессе генерации автоколебаний поступает радиочастотный сигнал, мгновенное напряжение которого
\begin{equation} \label{GrindEQ__1_} u_{g} (t)=U_{0} \cos (2\pi f_{0} t+\phi _{0e} ) {}, (1) \end{equation}
где $U_{0} =U_{0M} =U_{0F} $, ${}_{ }$ -- амплитуда автоколебаний на входе модулятора МЦ или выходе фильтра Ф, ${}_{ }$-- радиочастота автоколебаний, $\phi _{0e} $-- постоянный фазовый сдвиг.
В дальнейшем изложении рассмотрим ЛАГ, в котором лазер является высококогерентным источником оптического излучения и ширина линии $\Delta \nu _{L} \ll f_{0} $. Модулятор Маха-Цендера представляет собой два полосковых оптических волновода, соединенных на входе и выходе Y -- оптическими ответвителями (рис.1). При использовании в оптоэлектронном генераторе ЛАГ одиночного волоконного световода (ВС), разница в задержек $T_{{\rm M20}} $и $T_{{\rm M10}} $ в каналах модулятора составляет
\begin{equation} \label{GrindEQ__2_} {\rm \; }\Delta T_{{\rm M}} {\rm \; =\; }T_{{\rm M20}} {\rm -\; }T_{{\rm M10}}{}{},(2) \end{equation}
Волоконная оптическая линия задержки в ЛАГ является в общем случае дисперсионной, то есть время задержки в ВС является функцией оптической частоты лазера
\[T_{{\rm BC}} =T_{{\rm BC}} {\rm (}\nu _{} {\rm )}{},{} (3)\]. Таким образом, оптоэлектронный генератор ЛАГ представляет замкнутую автоколебательную систему с диссипацией, в состав которой входит дисперсионная линия задержки. }
2.Математическая модель ЛАГ
Для выявления основных механизмов формирования радиочастотного спектра в системе ЛАГ ниже представлены результаты анализа систем дифференциальных уравнений с флуктуациями для лазера и автогенератора.
2.1 Лазер в оптоэлектронном генераторе ЛАГ
Ниже приведем для отражения основных спектральных свойств лазера флуктуационные уравнения для него, выведенные с использованием полуклассической теории [ 17, 18, 19] . Динамический характер шумовых характеристик лазера можно описать с помощью уравнений для напряженности электрического поля $ E_{L} $ и оптической фазы $\varphi _{L} $ лазера
\begin{equation} \label{GrindEQ__4_} {\rm \; }dE_{L} {\rm /}dt{\rm \; =\; [}\alpha _{0L} -{\rm (2}\pi \nu _{0P} {\rm /}Q_{0L} )-\beta _{0n} E_{L} ^{2} ]E_{L} -\xi _{\beta AM},{}{}(4) \end{equation}
\begin{equation} \label{GrindEQ__5_} {\rm \; }[2\pi\nu _{0} - \Omega _{L} +d\varphi_{L} {\rm /}dt{\rm \; ]E_{L}=\; [}\sigma _{0L}E_{L} +\rho _{0L} E_{L} ^{3} ]-\xi _{\beta FM},{}{}(5) \end{equation}
где $\alpha _{0L} $ --оптическое усиление активной среды лазера,
$\nu _{0P}$ -- собственная частота резонатора лазера,
$Q_{0L} $ -- добротность резонатора лазера,
$\beta _{0n} $ --фактор спонтанного излучения активной среды,
$\Omega _{L}$ -- угловая оптическая частота продольной генерируемой моды резонатора лазера $\Omega _{L} =2\pi c(n_{L} L_{0L} )^{-1}$ ,
$n_{L}$ -- показатель преломления материала ,
$L_{0L}$ --геометрическая длина резонатора лазера,
$c$- скорость света в вакууме,
$\varepsilon _{{\rm 0}}$ - диэлектрическая постоянная,
$\sigma _{{\rm 0}}$, $\rho _{0L}$ -постоянные коэффициенты,
$\xi _{\beta AM} $, $\xi _{\beta FM}$ -- синфазная и квадратурная составляющие «ланжевеновских» фазовых флуктуаций.
Их спектральные плотности равны соответственно $S_{\beta AM}$ и $S_{\beta FM}$ , которые определяются шумами поля атомов активной среды в резонаторе лазера.
С учетом генерации лазера в ограниченной полосе оптических частот случайный процесс оптического излучения лазера можно считать стационарным с нулевым средним значением. Для такого процесса спектральные плотности $S_{mL} {\rm (}\nu {\rm )}$ и $S_{\psi L} {\rm (}\nu {\rm )}$ флуктуаций лазера $m_{L} (t)$ , $\psi _{m} (t)$ находятся при решении укороченных уравнений (4 ) и (5) с учетом флуктуационных «ланжевеновских» воздействий $S_{\beta AM}$, $S_{\beta FM}$ и составляют спектр лазера. Спектральную линию излучения лазера принято приближенно описывать функцией Лоренца, в которой ширина полоса излучения лазера равна $\Delta \nu$.
С выхода лазера линейно поляризованное оптическое излучение $E_{L}^{} $ поступает на вход модулятора МЦ. При этом зависимость от времени $t$ мгновенной напряженности поля излучения $E_{L}^{} $ на центральной частоте $\nu _{0} $ генерации лазера с учетом амплитудных и фазовых флуктуаций лазера определяется выражением
\[{\rm \; }E_{L} {\rm \; =\; (}E_{0L} {\rm +}m_{L} )\exp [j(2\pi \nu _{0} t-\varphi _{0L} -\psi _{m} )] {}{}, (8)\]
где ${\rm \; }m_{L} {\rm \; =\; }m_{L} {\rm (}t,R)$, ${\rm \; }\psi _{m} {\rm \; =}\psi _{m} {\rm (}t,R)$ -- амплитудные и фазовые флуктуации поля $E_{L}^{} $ лазера, определяемые спектральными плотностями выражений (6) и (7) , соответственно , $R$ -- индекс, учитывающий пространственную зависимость оптического излучения лазера, ${\rm \; }E_{0L} {\rm \; =\; }E_{0L} {\rm (}R)$ -- парциальная амплитуда излучения лазера ${\rm \; }\varphi _{0L} {\rm \; =}\varphi _{0L} {\rm (}R)$ -- парциальный фазовый набег напряженности излучения лазера.

Рис.2. Спектральная плотность мощности оптического излучения лазера накачки в ЛАГ в зависимости от отстройки V при различных значениях разности оптических частот. V=Δν=ν - ν0 ,а ν и ν0- текущая и центральная оптическая частота излучения лазера. Компьютерное моделирование производилось при Δν/ ν0= 10-10(кривая 1), 10-8 (кривая 2); 10-7(кривая 3).
2.2 Модулятор в ЛАГ
Оптическое излучение лазера проходит модулятор МЦ , волоконный световод ВС и поступает на приемную площадку фотодиода ФД. На площадке фотодиода ФД складываются два оптических излучения, прошедшие модулятор МЦ по первому $ {\rm \; }E_{1L} {\rm \; =\; }E_{1L}(R)$ и второму $ {\rm \; }E_{2L} {\rm \; =\; }E_{2L}(R)$ оптическим каналам
\begin{equation} \label{GrindEQ__9_} {\rm \;} E_{1L} {\rm =\; }k_{01} \cdot {\rm (}E_{0L} {\rm +}m_{L} )\exp [j2\pi \nu _{0} (t+T_{M1} +T_{{\rm BC}} )-j\varphi _{0L} -j\psi _{m1}] (9)\end{equation}
\begin{equation} \label{GrindEQ__10_} {\rm \;} E_{2L} {\rm =\; }k_{02} \cdot {\rm (}E_{0L} {\rm +}m_{L} )\exp [j2\pi \nu _{0} (t+T_{M2} +T_{{\rm BC}} )-j\varphi _{0L} -j\psi _{m2}] (10)\end{equation}
При малой амплитуде напряжения входного сигнала модуляции на МЦ можно воспользоваться линеаризацией аргумента ${\rm arg}_{12L} $ и для удобства в введен коэффициент передачи модулятора МЦ $M_{z} $ равный ${\rm \; }M_{z} {\rm =}k_{01} \cdot \{ 1-\cos {\rm \; }[2\pi \nu _{0} (T_{M20} -T_{M10} )]\}^{1/2}$.
2.3 Спектральная плотность $S{}_{\boldsymbol{\mu} }( \boldsymbol{\omega})$ продетектированных флуктуаций лазера
В результате фотодетектирования на выходе фотодиода ФД в процессе установления автоколебаний в замкнутой системе ЛАГ формируется гармонический радиочастотный сигнал на частоте $f_{0} $ с шумами. Радиочастотные шумы в ЛАГ, обусловленные шумами лазера, можно интерпретировать как преобразование флуктуаций. Можно считать, что в оптической части ЛАГ модулятором МЦ и световодом образован интерферометр с разными геометрическими длинами плеч. Интерферометр совместно с фотодиодом преобразует частотный(или фазовый) шум лазера в фазовые шумы фототока. Шум на выходе ФД в разомкнутой системе ЛАГ определяется конверсионными продетектированными АМ-ФМ шумами лазера $S_{\mu AM-FM} $ ,ФМ шумами лазера $S_{F} {\rm (}\omega {\rm )}$ и АМ шумами $S_{\mu AM} $ лазера. АМ шумами, как правило, можно пренебречь из-за их малости. В результате проведенного анализа спектральная плотность флуктуации токов, определяемая шумами лазера, на выходе фотодиода в разомкнутой системе ЛАГ равна
\[{ \ \; } S_{\mu}(\omega)= S_{\mu AM} {\rm \; }+S_{\mu AM-FM} +S_{F} \]
\begin{equation} \label{GrindEQ__12_} {\rm \; \; }S_{\mu AM} {\rm (}\omega _{} {\rm )=\; }\frac{S_{\beta AM} D_{AM} \cdot U_{0M}^{2} }{(\omega _{} -\omega _{0} )^{2} T_{0L}^{2} \cdot 0,25+B_{L}^{2} } {},{} (11) {\rm \; \; }S_{\mu AM-FM} {\rm =\; \; }\frac{4\cdot S_{\beta _{} } D_{FA} \cdot U_{0}^{2} \cdot \sin [2\pi \nu _{0} (T_{M1} -T_{M2} )]\cdot G_{12} }{(\omega _{} -\omega _{0} )^{2} T_{0L}^{2} \cdot B_{L}^{2} }{}, (12)\end{equation}
\begin{equation} \label{GrindEQ__13_} S_{F} {\rm (}\omega {\rm )\; }\approx \frac{4\cdot S_{\beta _{} } D_{FM} U_{0}^{2} \cdot G_{12} }{(\omega -\omega _{0} )^{2} T_{0L}^{2} \cdot B_{L}^{2} },{}{} (13)\end{equation}
где $G_{12} $ - коэффициент подавления фазовых флуктуаций оптического излучения лазера, который определяется как $G_{12} =1-[(\gamma _{1L\psi } -\gamma _{2L\psi } )+\exp (-\Delta T_{M} \cdot \Delta \nu _{L} )]^{} $, $\gamma _{1L\psi } $ и $\gamma _{2L\psi } $ -- пространственные постоянные флуктуаций фазы излучения лазера на выходе каналов ОК1 и ОК2 модулятора Маха-Цендера соответственно. На практике создать идеальные, идентичные оптические каналы в направленных ответвителях МЦ не удается и реально коэффициент подавления составляет$G_{12} \approx 10^{-1} -10^{-3} $ . Основными механизмами формирования шума на выходе фотодиода в разомкнутой системе ЛАГ с модулятором Маха-Цендера являются: преобразование или конверсия фазового шума лазера в амплитудный, подавление конверсионного и фазового шумов с коэффициентом $G_{12} $ за счет когерентного сложения колебаний с разными, но приближенно равными задержками на выходе фотодиода.
2.4 Дифференциальные уравнения оптоэлектронного генератора ЛАГ с флуктуациями
Дифференциальное уравнение для ЛАГ с учетом продетектированных флуктуаций оптической несущей выведено в предположении, что нелинейность усилителя НУ определяется средней крутизной $S_{{\rm HY}} $, а параметры фильтра - собственной частотой $f_{F0} $ и постоянной времени $T_{F} $ соответственно. При этом амплитуда автоколебаний $u(t)$ ЛАГ определяется как
\begin{equation} \label{GrindEQ__14_} {\rm \; }\frac{d^{2} u}{dt^{2} } {\rm +}\frac{1}{T_{F} } \cdot \frac{d^{} u}{dt} {\rm +\; 2}\pi f_{F0} u{\rm =\; }S_{{\rm HY}} [E_{0L}^{2} K_{BLZ} \cdot u(t-T_{BC} )]+\Psi _{n}{} {}, {} (14) \end{equation}
где $\Psi _{n} $ - шумовая составляющая напряжения на выходе фотодиода, образованная продетектированными флуктуациями фазы и амплитуды оптической несущей лазера, причем $\Psi _{n} =S_{{\rm HY}} \cdot K_{BLZ} \cdot \mu _{n} $. Дифференциальное флуктуационное уравнение совместно с (4-5) для лазера образует полную систему уравнений с флуктуациями. Они позволяют находить решения для радиочастотных спектров при разных величинах ширины линии лазера $\Delta \nu _{} $, которые представлены на рис.3 - 6 .
2.5 Спектр радиочастотных колебаний оптоэлектронного генератора ЛАГ
Используя выражения (11)- (13) и уравнения (14) также получено приближенное выражение для спектральной плотности мощности фазового шума ЛАГ ${\rm \; }S_{\Psi AG} $ от частотной отстройки $\omega -\omega _{0} $:
\begin{equation} \label{GrindEQ__15_} S_{\Psi AG} {\rm (}\omega _{} {\rm )=\; }\frac{4(\Delta \nu )^{2}S_{\beta }k_{E}D_{FM}G_{12} (1+\sin (\nu _{0} \cdot \Delta T_{M} )}{ (\omega _{} -\omega _{0} )^{2}T_{0L}^{2} \cdot \left|K_{BLZ} \right|\cdot E_{0L}^{2} \cdot [1+\cos (\omega -\omega _{0} )T_{BC} ]^{2} }.{}{}{} (15)\end{equation}
Выражение (15) устанавливает связь ${\rm \; }S_{\Psi AG} $ с шириной спектральной линии излучения лазера $\Delta \nu $, разницей задержек в МЦ $\Delta T_{{\rm M}} $, задержкой ВС $T_{BC}^{} $ и мощности лазера. Влияние ширины линии лазера $\Delta \nu $ на спектр $S_{\Psi AG} (\omega )$особенно проявляется при отстройках от несущей $\omega -\omega _{0} \approx 2\pi \cdot \Delta \nu _{} $ сравнимых с $\Delta \nu _{} $. При больших отстройках $\omega -\omega _{0} \gg 2\pi \cdot \Delta \nu _{} $ спектр $S_{\Psi AG} (\omega )$ определяется временем запаздывания $T_{BC} $ в световоде.
При большой разнице задержек в каналах модулятора, например, при $\Delta T_{{\rm M}} =10^{-4} c$ , при $T_{BC}^{} =10^{-9} c$, $\Delta \nu _{} \approx 10^{3}$Гц из (19) следует ,что
\begin{equation} \label{GrindEQ__16_} {\rm \; }\Delta f_{0,5} \approx 3,8\cdot \Delta \nu _{} ^{3/4}{}{}.(16) \end{equation}
В этом случае при выборе $(\Delta T_{M} \cdot \Delta \nu _{} )\to 1$ с помощью ЛАГ можно производить измерения ширины спектральной линии лазера $\Delta \nu _{} ^{} {\rm \; }\approx [\Delta f_{0,5}^{4/3} ]/3,8^{4/3} $.
Напротив, при малой разнице задержек в каналах модулятора, то есть когда произведение $(\Delta T_{M} \cdot \Delta \nu )\to 0$, ЛАГ является малошумящим автогенератором с предельно низким уровнем фазового шума. Например, при малой разнице задержек в каналах модулятора $\Delta T_{{\rm M}} =10^{-12} с $, $\Delta \nu \approx 10^{3} $Гц , $T_{BC}^{} =10\cdot 10^{-6} $ с,$G_{R} =0,999$, $S_{\beta _{} } \cdot D_{FM} =10^{-12} $ ширина спектральной линии ЛАГ примерно на четыре порядка меньше ширины линии лазера
\begin{equation} \label{GrindEQ__17_} {\rm \; }\Delta f_{0,.5} \approx 3,8\cdot 10^{-4} \cdot \Delta \nu _{} ^{3/4} {}(17). \end{equation}
3. Результаты компьютерного моделирования ЛАГ
Решение уравнения (14) позволило найти спектры напряжения автоколебаний $u_{g} (t)$ ЛАГ с помощью численных методов, используя прикладные программы пакета MATLAB, для разных значений ширины спектральной линии лазера (рис.3) и разных величинах задержек $T_{BC}^{} $ . На рис.3 представлены спектральные плотности мощности фазовых флуктуаций лазера, взятые при численном моделировании при ширине полосы излучения лазера $\Delta v$= 10кГц (кривая 1), 1 МГц (кривая 2); и 10 МГц (кривая 3) при $v_{0} =1,29\cdot 10^{14} $${}^{ }$Гц. При этом спектры приближенно описывались функцией Лоренца.
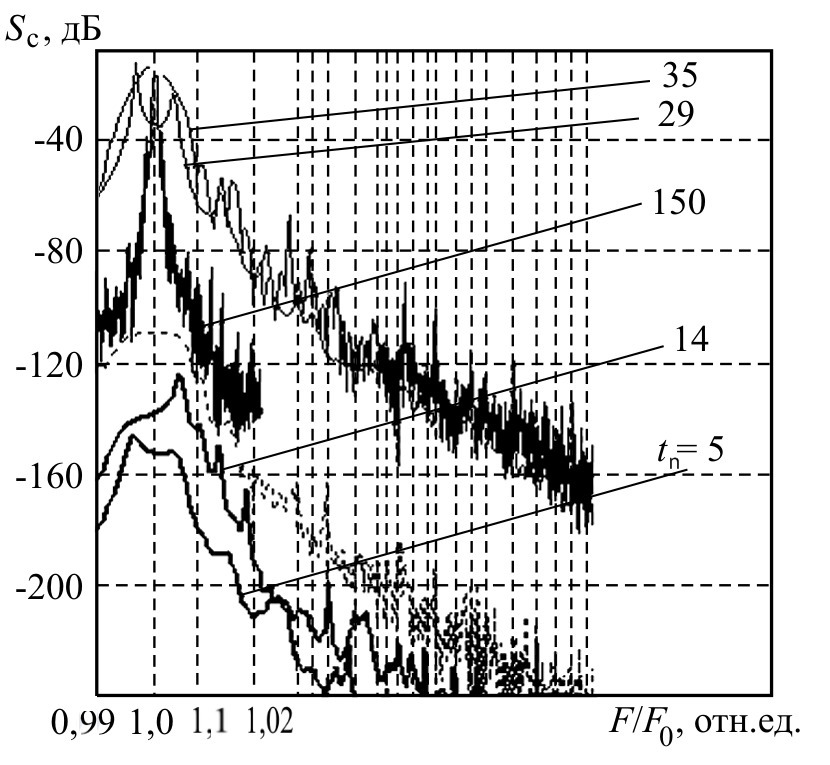
Рис.3 Спектральная плотность мощности фазового шума радиочастотных автоколебаний ЛАГ от относительной отстройки для разных величин нормированного времени наблюдения переходного процесса поднесущей t 0 =5, 14, 29, 35, 150 . где t 0 , нормированное время начала развития колебаний радиочастотных колебаний в оптоэлектронном генераторе ЛАГ. Нормированное время от начала отсчета на время задержки в ВОЛЗ t 0 = t / T BZ . Компьютерное моделирование производилось при значениях Δν/ ν0=10-6 , Δν=129 МГц , ν0 =129 · 1012 Гц .
Был изучен вопрос формирования спектра поднесущей ЛАГ и получены решения спектра поднесущей для различных времен переходного процесса (рис. 3) (для ширины спектра лазера $\Delta v$=129 МГц , $\Delta v/v_{0} $ =10${}^{-6}$ , $v_{0} =1,29\cdot 10^{14} $${}^{ }$Гц ). На рис. 3 видно, что процесс формирования и установления спектра ЛАГ занимает продолжительное время кратное примерно 100 временам задержки в световоде.
На рис. 4 и рис.5 показаны результаты численного моделирования спектральной плотности фазовых шумов для ЛАГ с недисперсионной и дисперсионной линией задержки. В результате исследования сделаны выводы, что при малых задержках в световоде на спектр ЛАГ с недисперсионной линией задержки оказывает значительное влияние шумы, связанные с фазово-амплитудной конверсией (рис. 4). При увеличении ширины линии лазера$\Delta v$ в спектре ЛАГ появляются дополнительные шумовые составляющие.

Рис.4. Спектральная плотность мощности фазового шума радиочастотных автоколебаний ЛАГ с недисперсионной ВОЛЗ от отстройки по радиочастоте от поднесущей 8,2 ГГц при разных значениях ширины спектральной плотности оптического излучения лазера. Компьютерное моделирование на основе флуктуационных уравнений (18) ЛАГ при Δν= 10кГц (кривая 1), 1 МГц (кривая 2); и 10 МГц (кривая 3)при ν0 =129 · 1012 Гц. Дисперсионная крутизна запаздывания в световоде составляла 10-7 , длина световода -200 м. Зависимости при Δν = 50 МГц (кривая 4) и при Δν =10 кГц (кривая 5) .

Рис.5 Спектральная плотность мощности фазового шума от относительной отстройки (радиочастотная поднесущая) автоколебаний ЛАГ с дисперсионной волоконно-оптической линией задержки. Дисперсионная крутизна запаздывания в световоде , длина световода L=1000 м. Компьютерное моделирование на основе флуктуационных уравнений (18) ЛАГ при Δν= 10кГц (кривая 1), 1 МГц (кривая 2); и 100 МГц (кривая 3).
В ЛАГ с дисперсионной линией задержки увеличение ширины спектра лазера (рис. 5) более чем 100 МГц приводит за счет дисперсии волоконного световода к значительному расширению спектра ЛАГ. За счет дисперсии световода спектр имеет замечательную особенность - гребенчатую структуру - периодическую зависимость от отстройки по радиочастоте. Период данной зависимости пропорционален произведению времени дисперсии в световоде на ширину полосы излучения лазера $DF\sim \Delta v\cdot \tau _{D} $ . При использовании высоко дисперсионных световодов или низко когерентных лазеров с шириной линии более 100 МГц в спектральной линии генерации ЛАГ наблюдаются осцилляции по частоте отстройки. Такая гребенчатая структура радиочастотного спектра ЛАГ является похожей на структуру оптических спектров лазерных диодов с высоко дисперсионными активными средами.
4.Экспериментальное исследования
Были экспериментально исследованы несколько опытных образцов ЛАГ диапазона СВЧ с разными лазерными диодами накачки, излучающие на длинах волн 1310 нм или 1550нм с максимальной выходной мощностью оптического излучения примерно от 10 до 20 мВт. На рис.1 (б) представлено фото одного из образцов, собранного по схеме рис. 1(а). В качестве фотодетектора был применен фотодиод ФД на основе InGaAs. Радиочастотный фильтр представлял собой диэлектрический резонатор СВЧ с нагруженной добротностью $Q\approx 1000$, выполненный на керамике и собственной частотой примерно 8,2 ГГц. В макете имела место широкополосная до $15$ ГГц, модуляция лазерного излучения, которая осуществлялась модулятором Маха-Цендера фирмы Hitachi. При проведении экспериментов использовались одномодовые световоды с длинами от 60 м до 4640 м. Экспериментальные амплитудные и частотные регулировочные кривые приведены на рис. 6. При разных длинах в системе ЛАГ получено устойчивая генерация одночастотных автоколебания на частоте близкой к 8,2 ГГц. На рис.6 в в экспериментальных частотных зависимостях от тока накачки лазерного диода можно наблюдать скачки частоты (рис. 6 в ), что связано с перестройкой частоты на соседние типы колебаний. В ЛАГ получена кратковременная (на интервале времени 1 мин.) относительная нестабильность частоты (среднеквадратичная по Аллану) генерируемой поднесущей не хуже $1\cdot 10^{-8} $ при комнатной температуре. Уровень фазовых шумов при использовании различных лазеров накачки составил величину $S_{c} \approx $- 80---140 дБ/Гц на отстройках 1-10 кГц от частоты генерируемой СВЧ поднесущей (рис.4) и зависел от ширины линии излучения лазера. Данные экспериментальные зависимости хорошо согласуются с расчетными при учете стабилизационного эффекта на длинах волоконного световода больше 50 м. Не соответствие расчетных и экспериментальных кривых фазовых шумов $S_{c} $ объясняется влиянием на них поляризации и неоднородности по пространству излучения реальных лазерных источников, которые не учитывались при расчете.
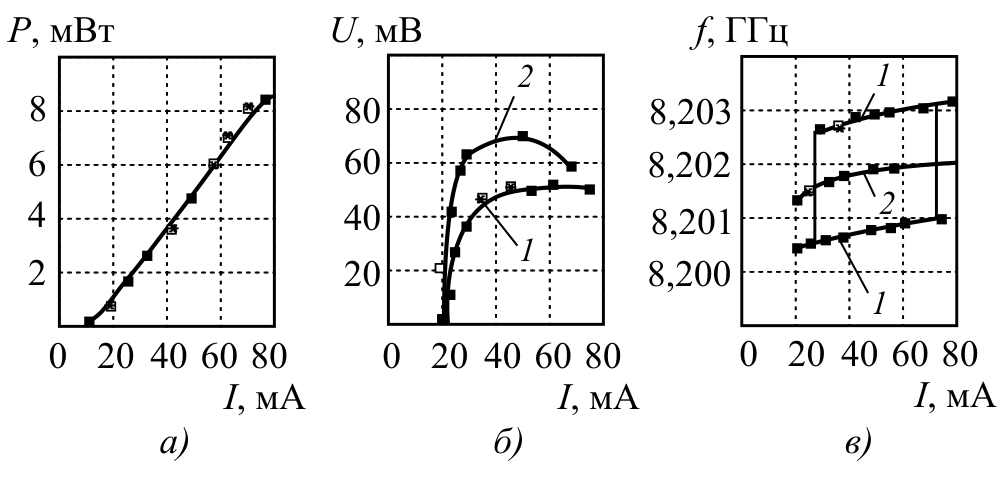
Рис.6 Экспериментальные зависимости в ЛАГ СВЧ диапазона от тока смещения а) мощности лазерного диода , б) амплитуды напряжения автоколебаний при средней радиочастоте автоколебаний =8,2 ГГц, в) радиочастоты автоколебаний для различных длин световодов 60м (1)и 70 м (2).
5.Выводы и заключение.
Проведенный анализ показал, что спектр оптоэлектронного генератора ЛАГ определяют продетектированные конверсионные фазово-амплитудные шумы и фазовые флуктуации шумы оптического излучения лазера. Величина спектральной плотности мощности ЛАГ пропорциональна квадрату ширины линии оптического излучения лазера. Увеличение ширины спектральной линии лазера накачки приводит к расширению радиочастотного спектра ЛАГ. При условии соответственно малой и большой разнице задержек в каналах модулятора МЦ ЛАГ можно соответственно использовать в качестве малошумящего автогенератора с рекордно малыми уровнями фазового шума или\textit{ измерителя малых ширин спектральной линии излучения лазеров менее 10кГц .
6.Благодарности
Авторы выражают благодарность за проявленный интерес и участие в дискуссиях профессору Удалову Н.Н. и профессору Капранову М.В.
7. Литература:
1.Nakazawa M., Nakashima T., Tokuda M. An optoelectronic self-oscillatory circuit with an optical fiber delayed feedback and its injection locking technique. // J/ Lightwave Technol. -- 1984. -- V.2, №5, - P. 719-730.
2. Григорьянц В.В., Дворников А.А., Ильин Ю.Б. и Константинов В.Н. Прокофьев В. А. Генерация радиосигналов в системе ``лазер-оптическая линия задержки''. // Квант. электрон. -- 1984. -- Т.11, №4. -- С. 766-775.
3. Grigor'yants V.V., Il'in YU.B.. Laser optical fibre heterodyne interferometer with frequency indicating of the phase shift of a light signal in an optical waveguide.// Optical and quantum electronics.-1989.-№ 21.-P.423-427.
4.Борцов А. А., Григорьянц В. В., Ильин Ю. Б. Влияние эффективности возбуждения световодов на частоту автогенератора с дифференциальной волоконно-оптической линией задержки // Радиотехника. -- 1989 г. -- № 7. -- С.84--89.
5.А.с.№1538265 СССР, МКИ3 H03K 9/00А. Устройство функционального преобразования в частоту / Борцов А. А., Ильин Ю. Б. и др. (СССР). -- 9 c.-1989 г.
6. X. S. Yao and L. Maleki, ``Optoelectronic microwave oscillator,'' \textit{J. Opt.Soc. Amer. B, Opt. Phys.}, vol. 13, no. 8, pp. 1725--1735, 1996.
7.Борцов А. А., Ильин Ю. Б. Разностный оптоэлектронный автогенератор СВЧ с крайне низким уровнем фазовых шумов // Радиооптические технологии в приборостроении: Тез.докл. II-ой научн.-техн. конф. 14--21 сентября 2004г. -- Сочи, 2004 г. -- С.84--86.
8. J. J. McFerran, E. N. Ivanov, A. Bartels, G. Wilpers, C. W. Oates, S. A. Diddams, and Hollberg, ''Low-noise synthesis of microwave signals from an optical source,'' Electron. Lett. 41, 650-651 (2005).
9. Savchenkov, A. A. Ilchenko \textit{et al. }Low Threshold optical oscillations in a whispering gallery mode CaF2 resonator. Physical Review Letters 93, 243905 (2004).
10. Царапкин Д.П. --Методы генерирования СВЧ колебаний с минимальным уровнем фазовых шумов: Диссертация на соискание доктора технических наук . -- М., 2004. --413 с.
11.Патент на изобретение №2282302 RU, МПК 3 7 Н03 С3/00. Формирователь частотно-модулированного сигнала / Борцов А. А., Ильин Ю. Б. -- 10 с. 2004г.
12.Патент на полезную модель №44902 RU, МПК${}^{3}$ 7 Н03 С3/00. Формирователь частотно-модулированного сигнала / Борцов А. А., Ильин Ю. Б. -- 10 с. 2004г.
13. A13. A. A. Savchenkov, A. B. Matsko, V. S. Ilchenko, and L.Maleki, ''Optical resonators with ten million finesse,'' Opt. Express \15, 6768-6773 (2007).
14.Борцов А. А. Управление частотой в лазерном автогенераторе с составной волоконно-оптической линией задержки // Автореф. канд. дис. на соиск. уч. степ. канд. техн. наук. -- М.:МЭИ. -- 2005. -- С.
15.Борцов А. А. Фазочастотная и амплитудно-частотная характеристики мезаполоскового квантово-размерного лазерного диода с полосой частот модуляции до 12 ГГц //Радиотехника -- 2006 г2006 г. -- С.43 -- 47
16. Лэкс М. Флуктуации и когерентные явления .М.:Мир,1974
17. Лебедев А.К. Теория лазера М.: МЭИ, 1998
18. Жалуд В., Кулешов В.Н.. Шумы в полупроводниковых устройствах.Под общей редакцией А.К.Нарышкина. -- М. : Советсткое радио,1977г.-416 с.
Статья поступила в редакцию журнала "Радиотехника" 8 июля 2008 года.
Журнал "РАДИОТЕХНИКА", 2010 г.,№2
{gallery}publication/Radote2010{/gallery}
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |





